Privacy-Preserving Distributed Machine Learning Made Faster
Paper and Code
May 12, 2022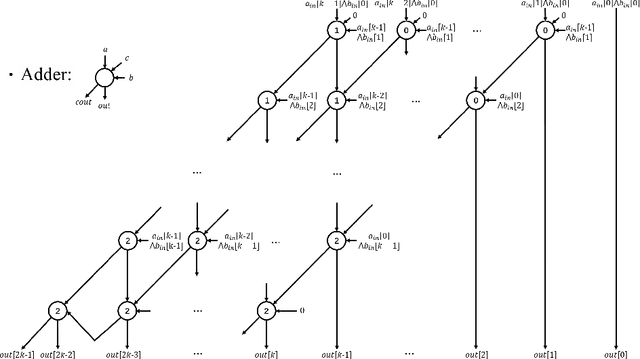
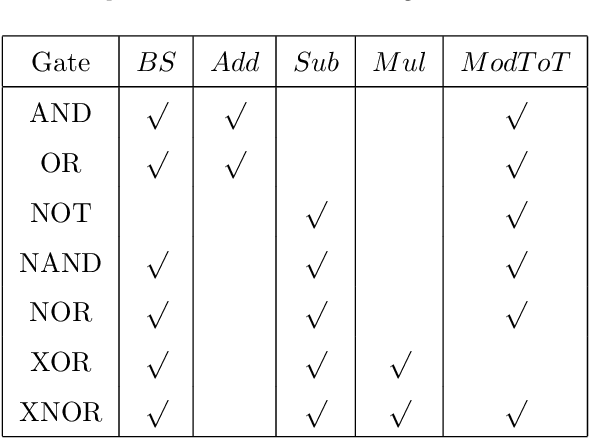
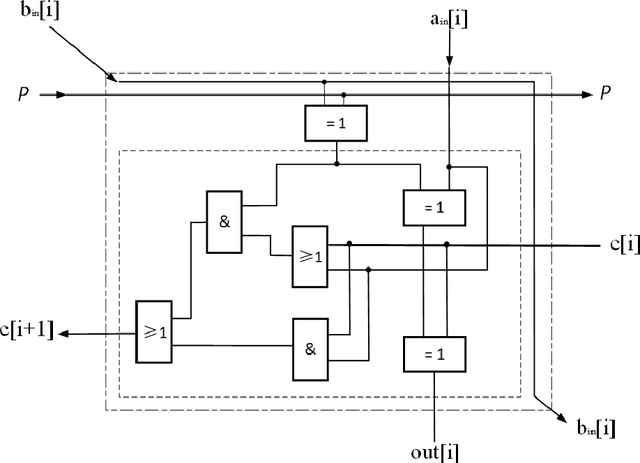
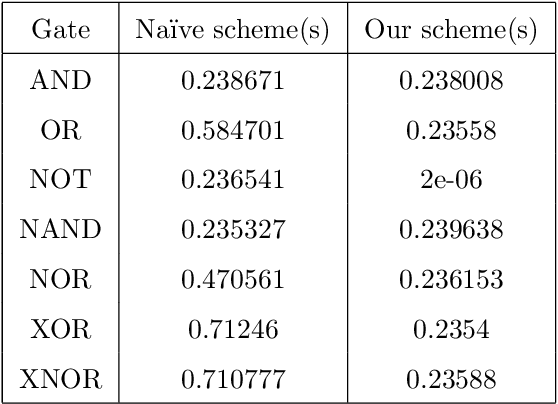
With the development of machine learning, it is difficult for a single server to process all the data. So machine learning tasks need to be spread across multiple servers, turning the centralized machine learning into a distributed one. However, privacy remains an unsolved problem in distributed machine learning. Multi-key homomorphic encryption is one of the suitable candidates to solve the problem. However, the most recent result of the Multi-key homomorphic encryption scheme (MKTFHE) only supports the NAND gate. Although it is Turing complete, it requires efficient encapsulation of the NAND gate to further support mathematical calculation. This paper designs and implements a series of operations on positive and negative integers accurately. First, we design basic bootstrapped gates with the same efficiency as that of the NAND gate. Second, we construct practical $k$-bit complement mathematical operators based on our basic binary bootstrapped gates. The constructed created can perform addition, subtraction, multiplication, and division on both positive and negative integers. Finally, we demonstrated the generality of the designed operators by achieving a distributed privacy-preserving machine learning algorithm, i.e. linear regression with two different solutions. Experiments show that the operators we designed are practical and efficient.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge