Prioritized training on points that are learnable, worth learning, and not yet learned

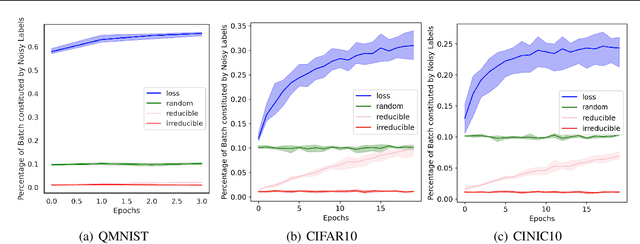
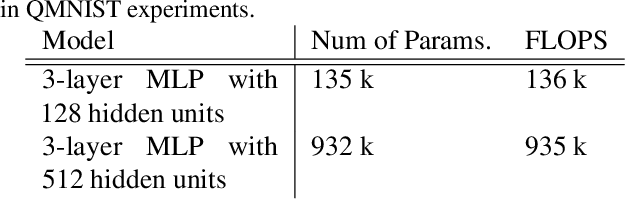
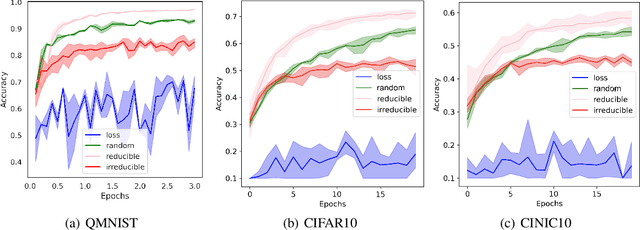
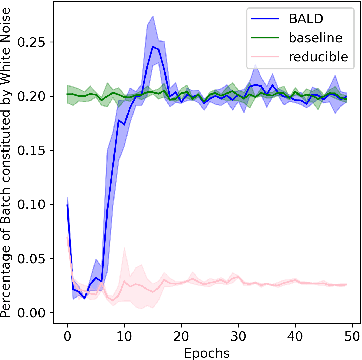
We introduce Goldilocks Selection, a technique for faster model training which selects a sequence of training points that are "just right". We propose an information-theoretic acquisition function -- the reducible validation loss -- and compute it with a small proxy model -- GoldiProx -- to efficiently choose training points that maximize information about a validation set. We show that the "hard" (e.g. high loss) points usually selected in the optimization literature are typically noisy, while the "easy" (e.g. low noise) samples often prioritized for curriculum learning confer less information. Further, points with uncertain labels, typically targeted by active learning, tend to be less relevant to the task. In contrast, Goldilocks Selection chooses points that are "just right" and empirically outperforms the above approaches. Moreover, the selected sequence can transfer to other architectures; practitioners can share and reuse it without the need to recreate it.