Precision Learning: Towards Use of Known Operators in Neural Networks
Paper and Code
Oct 12, 2018
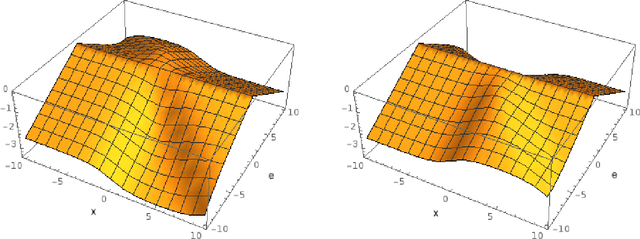
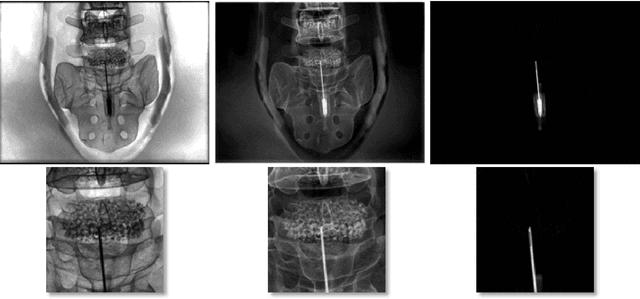
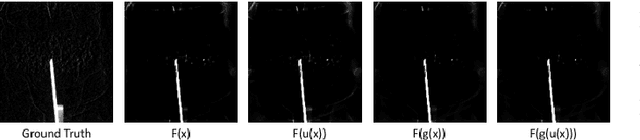
In this paper, we consider the use of prior knowledge within neural networks. In particular, we investigate the effect of a known transform within the mapping from input data space to the output domain. We demonstrate that use of known transforms is able to change maximal error bounds. In order to explore the effect further, we consider the problem of X-ray material decomposition as an example to incorporate additional prior knowledge. We demonstrate that inclusion of a non-linear function known from the physical properties of the system is able to reduce prediction errors therewith improving prediction quality from SSIM values of 0.54 to 0.88. This approach is applicable to a wide set of applications in physics and signal processing that provide prior knowledge on such transforms. Also maximal error estimation and network understanding could be facilitated within the context of precision learning.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge