Position-Aware Subgraph Neural Networks with Data-Efficient Learning
Paper and Code
Nov 01, 2022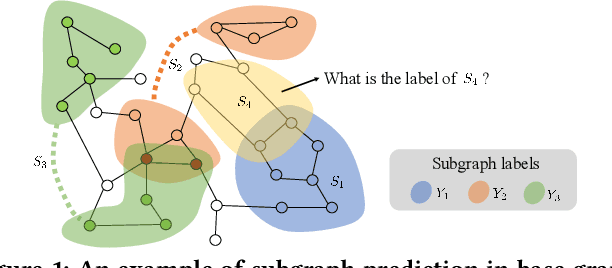
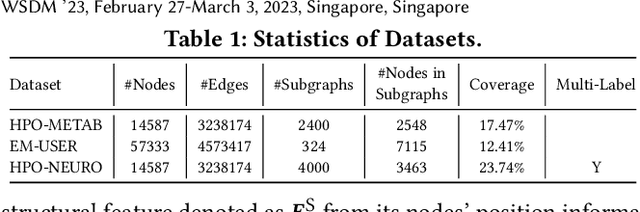
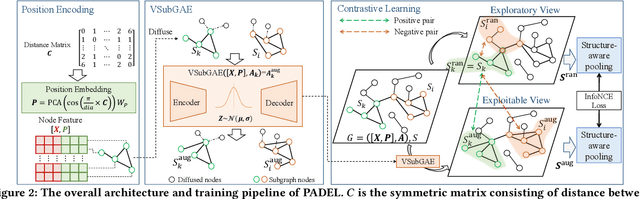
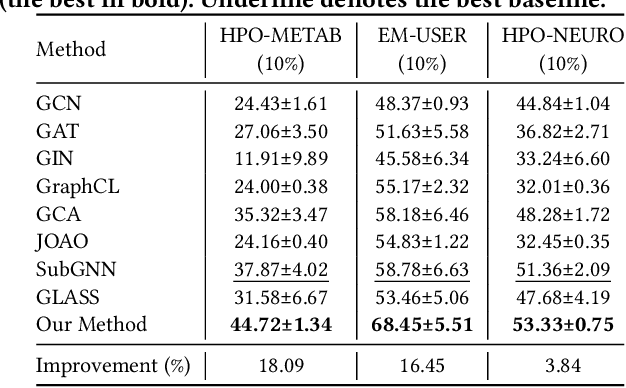
Data-efficient learning on graphs (GEL) is essential in real-world applications. Existing GEL methods focus on learning useful representations for nodes, edges, or entire graphs with ``small'' labeled data. But the problem of data-efficient learning for subgraph prediction has not been explored. The challenges of this problem lie in the following aspects: 1) It is crucial for subgraphs to learn positional features to acquire structural information in the base graph in which they exist. Although the existing subgraph neural network method is capable of learning disentangled position encodings, the overall computational complexity is very high. 2) Prevailing graph augmentation methods for GEL, including rule-based, sample-based, adaptive, and automated methods, are not suitable for augmenting subgraphs because a subgraph contains fewer nodes but richer information such as position, neighbor, and structure. Subgraph augmentation is more susceptible to undesirable perturbations. 3) Only a small number of nodes in the base graph are contained in subgraphs, which leads to a potential ``bias'' problem that the subgraph representation learning is dominated by these ``hot'' nodes. By contrast, the remaining nodes fail to be fully learned, which reduces the generalization ability of subgraph representation learning. In this paper, we aim to address the challenges above and propose a Position-Aware Data-Efficient Learning framework for subgraph neural networks called PADEL. Specifically, we propose a novel node position encoding method that is anchor-free, and design a new generative subgraph augmentation method based on a diffused variational subgraph autoencoder, and we propose exploratory and exploitable views for subgraph contrastive learning. Extensive experiment results on three real-world datasets show the superiority of our proposed method over state-of-the-art baselines.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge