Point-set Distances for Learning Representations of 3D Point Clouds

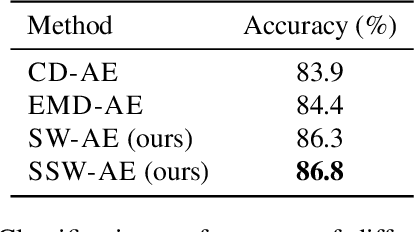
Learning an effective representation of 3D point clouds requires a good metric to measure the discrepancy between two 3D point sets, which is non-trivial due to their irregularity. Most of the previous works resort to using the Chamfer discrepancy or Earth Mover's distance, but those metrics are either ineffective in measuring the differences between point clouds or computationally expensive. In this paper, we conduct a systematic study with extensive experiments on distance metrics for 3D point clouds. From this study, we propose to use a variant of the Wasserstein distance, named the sliced Wasserstein distance, for learning representations of 3D point clouds. Experiments show that the sliced Wasserstein distance allows the neural network to learn a more efficient representation compared to the Chamfer discrepancy. We demonstrate the efficiency of the sliced Wasserstein metric on several tasks in 3D computer vision including training a point cloud autoencoder, generative modeling, transfer learning, and point cloud registration.