PGMHD: A Scalable Probabilistic Graphical Model for Massive Hierarchical Data Problems
Paper and Code
Aug 19, 2014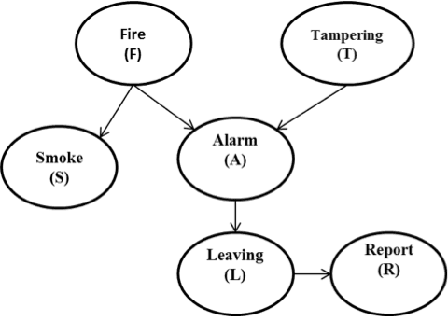
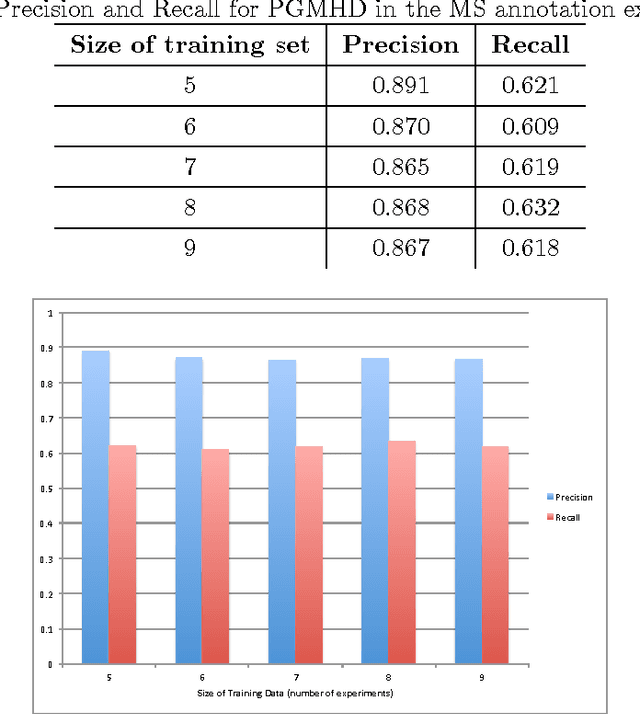
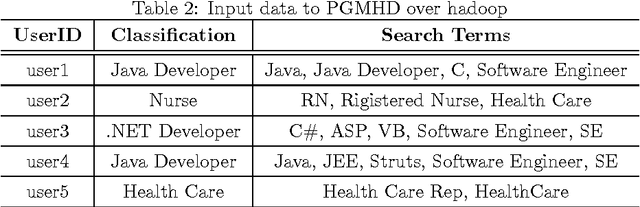
In the big data era, scalability has become a crucial requirement for any useful computational model. Probabilistic graphical models are very useful for mining and discovering data insights, but they are not scalable enough to be suitable for big data problems. Bayesian Networks particularly demonstrate this limitation when their data is represented using few random variables while each random variable has a massive set of values. With hierarchical data - data that is arranged in a treelike structure with several levels - one would expect to see hundreds of thousands or millions of values distributed over even just a small number of levels. When modeling this kind of hierarchical data across large data sets, Bayesian networks become infeasible for representing the probability distributions for the following reasons: i) Each level represents a single random variable with hundreds of thousands of values, ii) The number of levels is usually small, so there are also few random variables, and iii) The structure of the network is predefined since the dependency is modeled top-down from each parent to each of its child nodes, so the network would contain a single linear path for the random variables from each parent to each child node. In this paper we present a scalable probabilistic graphical model to overcome these limitations for massive hierarchical data. We believe the proposed model will lead to an easily-scalable, more readable, and expressive implementation for problems that require probabilistic-based solutions for massive amounts of hierarchical data. We successfully applied this model to solve two different challenging probabilistic-based problems on massive hierarchical data sets for different domains, namely, bioinformatics and latent semantic discovery over search logs.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge