Partial Sum Minimization of Singular Values Representation on Grassmann Manifolds
Paper and Code
Apr 28, 2017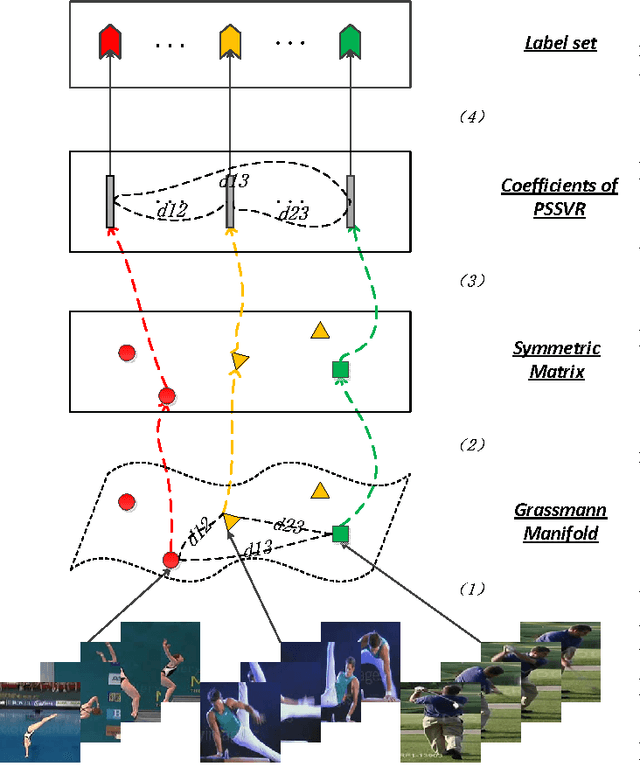
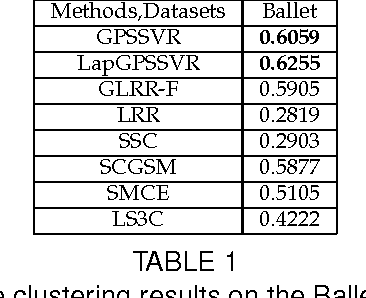


As a significant subspace clustering method, low rank representation (LRR) has attracted great attention in recent years. To further improve the performance of LRR and extend its applications, there are several issues to be resolved. The nuclear norm in LRR does not sufficiently use the prior knowledge of the rank which is known in many practical problems. The LRR is designed for vectorial data from linear spaces, thus not suitable for high dimensional data with intrinsic non-linear manifold structure. This paper proposes an extended LRR model for manifold-valued Grassmann data which incorporates prior knowledge by minimizing partial sum of singular values instead of the nuclear norm, namely Partial Sum minimization of Singular Values Representation (GPSSVR). The new model not only enforces the global structure of data in low rank, but also retains important information by minimizing only smaller singular values. To further maintain the local structures among Grassmann points, we also integrate the Laplacian penalty with GPSSVR. An effective algorithm is proposed to solve the optimization problem based on the GPSSVR model. The proposed model and algorithms are assessed on some widely used human action video datasets and a real scenery dataset. The experimental results show that the proposed methods obviously outperform other state-of-the-art methods.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge