Partial-Label Regression

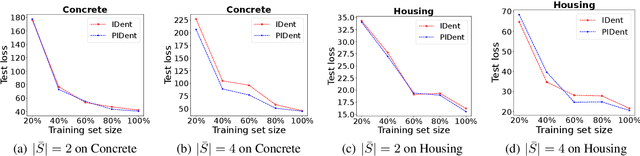
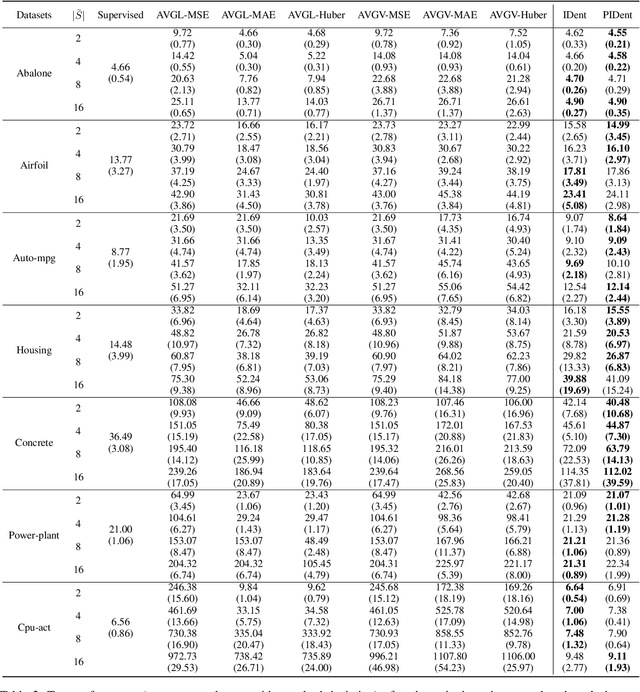
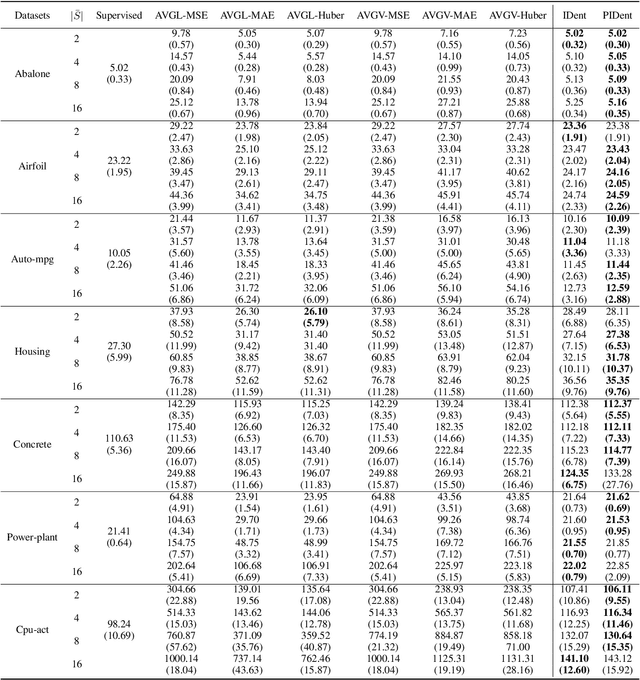
Partial-label learning is a popular weakly supervised learning setting that allows each training example to be annotated with a set of candidate labels. Previous studies on partial-label learning only focused on the classification setting where candidate labels are all discrete, which cannot handle continuous labels with real values. In this paper, we provide the first attempt to investigate partial-label regression, where each training example is annotated with a set of real-valued candidate labels. To solve this problem, we first propose a simple baseline method that takes the average loss incurred by candidate labels as the predictive loss. The drawback of this method lies in that the loss incurred by the true label may be overwhelmed by other false labels. To overcome this drawback, we propose an identification method that takes the least loss incurred by candidate labels as the predictive loss. We further improve it by proposing a progressive identification method to differentiate candidate labels using progressively updated weights for incurred losses. We prove that the latter two methods are model-consistent and provide convergence analyses. Our proposed methods are theoretically grounded and can be compatible with any models, optimizers, and losses. Experiments validate the effectiveness of our proposed methods.