Ordinal Pooling
Paper and Code
Sep 03, 2021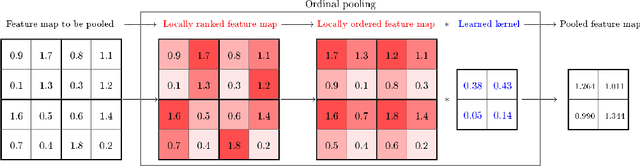

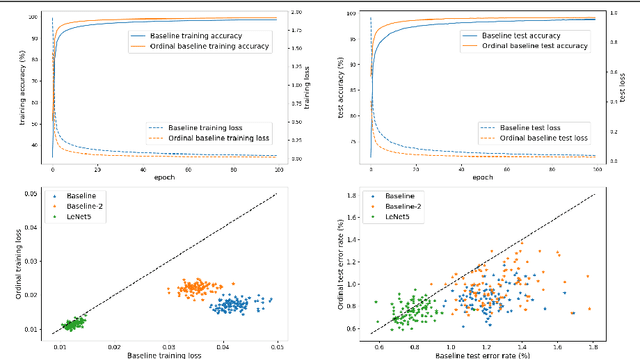

In the framework of convolutional neural networks, downsampling is often performed with an average-pooling, where all the activations are treated equally, or with a max-pooling operation that only retains an element with maximum activation while discarding the others. Both of these operations are restrictive and have previously been shown to be sub-optimal. To address this issue, a novel pooling scheme, named\emph{ ordinal pooling}, is introduced in this work. Ordinal pooling rearranges all the elements of a pooling region in a sequence and assigns a different weight to each element based upon its order in the sequence. These weights are used to compute the pooling operation as a weighted sum of the rearranged elements of the pooling region. They are learned via a standard gradient-based training, allowing to learn a behavior anywhere in the spectrum of average-pooling to max-pooling in a differentiable manner. Our experiments suggest that it is advantageous for the networks to perform different types of pooling operations within a pooling layer and that a hybrid behavior between average- and max-pooling is often beneficial. More importantly, they also demonstrate that ordinal pooling leads to consistent improvements in the accuracy over average- or max-pooling operations while speeding up the training and alleviating the issue of the choice of the pooling operations and activation functions to be used in the networks. In particular, ordinal pooling mainly helps on lightweight or quantized deep learning architectures, as typically considered e.g. for embedded applications.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge