Optimized Cartesian $K$-Means
Paper and Code
May 16, 2014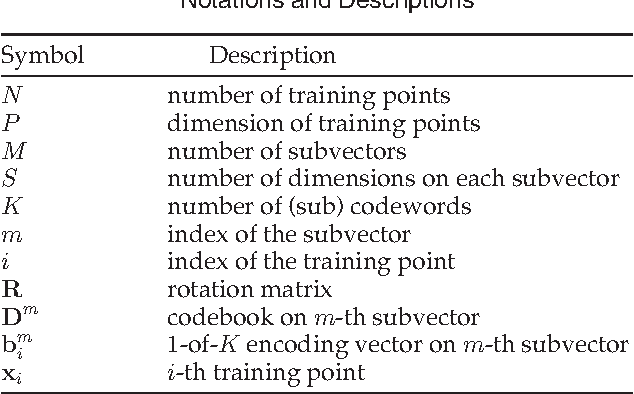
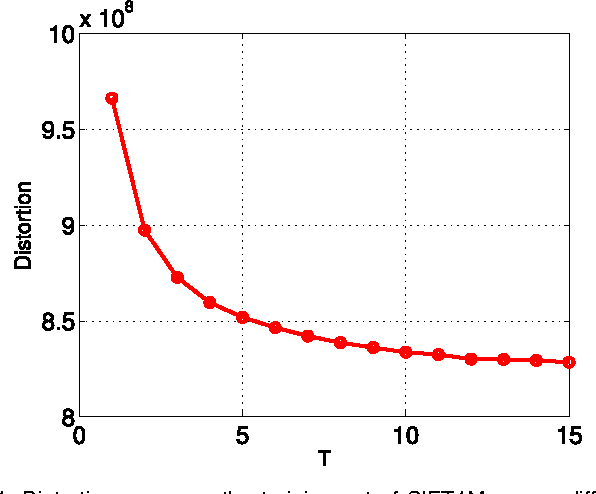
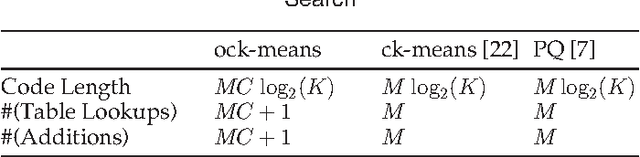
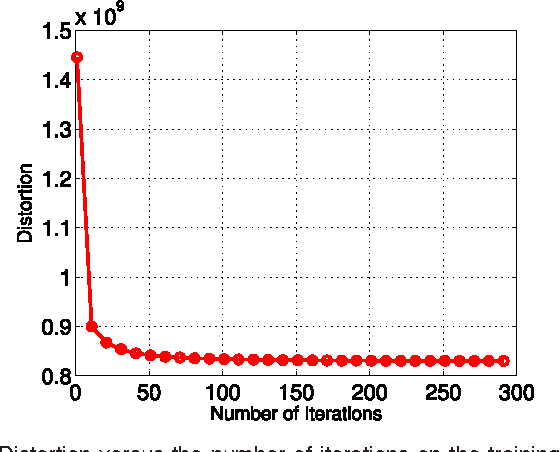
Product quantization-based approaches are effective to encode high-dimensional data points for approximate nearest neighbor search. The space is decomposed into a Cartesian product of low-dimensional subspaces, each of which generates a sub codebook. Data points are encoded as compact binary codes using these sub codebooks, and the distance between two data points can be approximated efficiently from their codes by the precomputed lookup tables. Traditionally, to encode a subvector of a data point in a subspace, only one sub codeword in the corresponding sub codebook is selected, which may impose strict restrictions on the search accuracy. In this paper, we propose a novel approach, named Optimized Cartesian $K$-Means (OCKM), to better encode the data points for more accurate approximate nearest neighbor search. In OCKM, multiple sub codewords are used to encode the subvector of a data point in a subspace. Each sub codeword stems from different sub codebooks in each subspace, which are optimally generated with regards to the minimization of the distortion errors. The high-dimensional data point is then encoded as the concatenation of the indices of multiple sub codewords from all the subspaces. This can provide more flexibility and lower distortion errors than traditional methods. Experimental results on the standard real-life datasets demonstrate the superiority over state-of-the-art approaches for approximate nearest neighbor search.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge