Optimal Decision Making Under Strategic Behavior

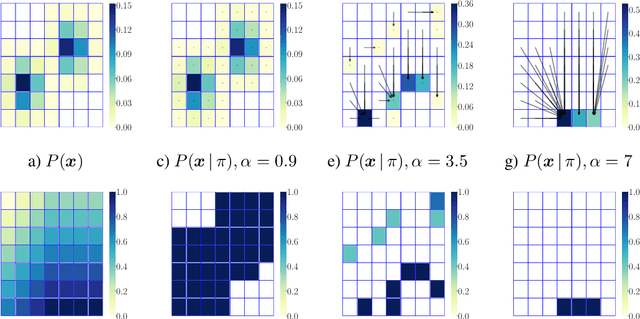
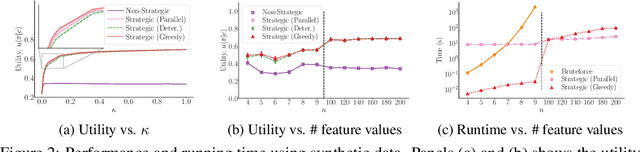
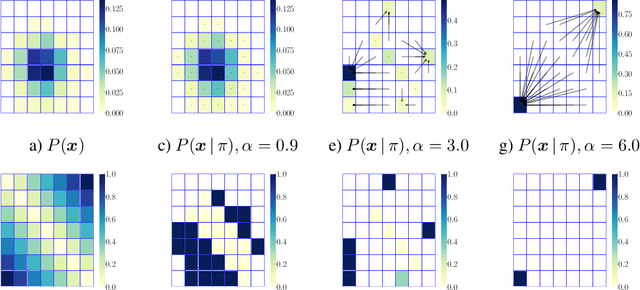
We are witnessing an increasing use of data-driven predictive models to inform decisions. As decisions have implications for individuals and society, there is increasing pressure on decision makers to be transparent about their decision policies, models, and the features they use. At the same time, individuals may use knowledge, gained by transparency, to invest effort strategically in order to maximize their chances of receiving a beneficial decision. In this paper, our goal is to find decision policies that are optimal in terms of utility in such a strategic setting. To this end, we first use the theory of optimal transport to characterize how strategic investment of effort by individuals leads to a change in the feature distribution at a population level. Then, we show that, in contrast with the non-strategic setting, optimal decision policies are stochastic, and we cannot expect to find them in polynomial time. Finally, we derive an efficient greedy algorithm that is guaranteed to find locally optimal decision policies in polynomial time. Experiments on synthetic and real lending data illustrate our theoretical findings and show that the decision policies found by our greedy algorithm achieve higher utility than deterministic threshold rules, which are optimal policies in a non-strategic setting.