On the Importance of the Kullback-Leibler Divergence Term in Variational Autoencoders for Text Generation
Paper and Code
Sep 30, 2019
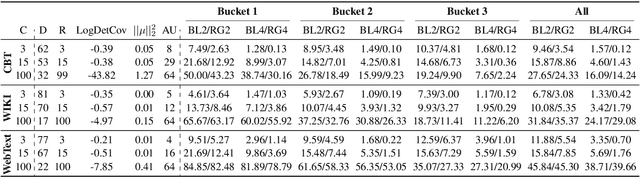
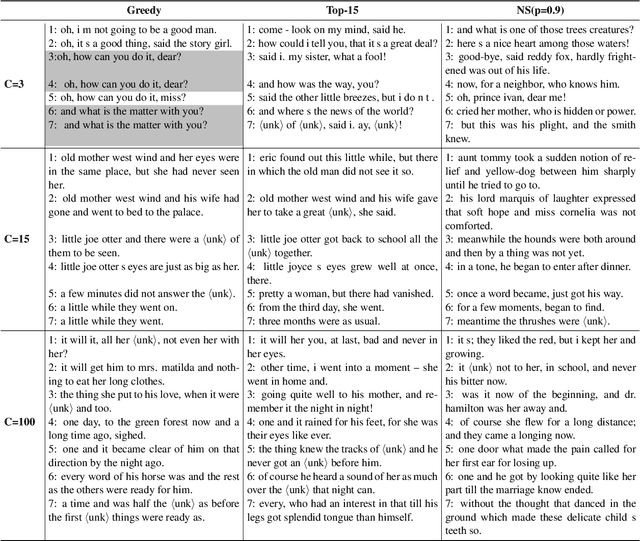
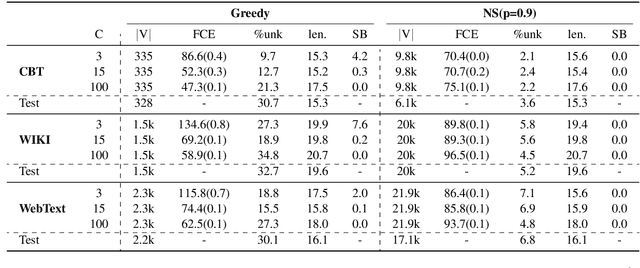
Variational Autoencoders (VAEs) are known to suffer from learning uninformative latent representation of the input due to issues such as approximated posterior collapse, or entanglement of the latent space. We impose an explicit constraint on the Kullback-Leibler (KL) divergence term inside the VAE objective function. While the explicit constraint naturally avoids posterior collapse, we use it to further understand the significance of the KL term in controlling the information transmitted through the VAE channel. Within this framework, we explore different properties of the estimated posterior distribution, and highlight the trade-off between the amount of information encoded in a latent code during training, and the generative capacity of the model.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge