On the Benefits of Multiple Gossip Steps in Communication-Constrained Decentralized Optimization
Paper and Code
Nov 20, 2020
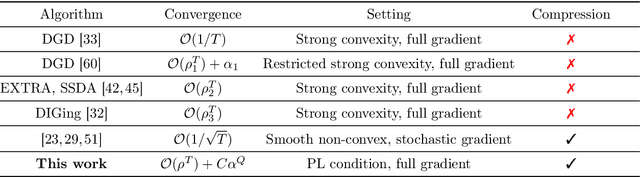

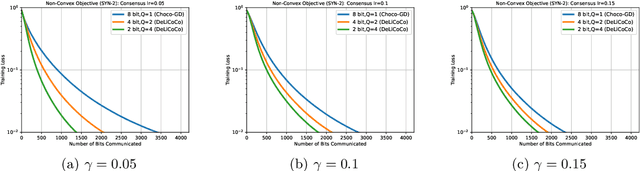
In decentralized optimization, it is common algorithmic practice to have nodes interleave (local) gradient descent iterations with gossip (i.e. averaging over the network) steps. Motivated by the training of large-scale machine learning models, it is also increasingly common to require that messages be {\em lossy compressed} versions of the local parameters. In this paper, we show that, in such compressed decentralized optimization settings, there are benefits to having {\em multiple} gossip steps between subsequent gradient iterations, even when the cost of doing so is appropriately accounted for e.g. by means of reducing the precision of compressed information. In particular, we show that having $O(\log\frac{1}{\epsilon})$ gradient iterations {with constant step size} - and $O(\log\frac{1}{\epsilon})$ gossip steps between every pair of these iterations - enables convergence to within $\epsilon$ of the optimal value for smooth non-convex objectives satisfying Polyak-\L{}ojasiewicz condition. This result also holds for smooth strongly convex objectives. To our knowledge, this is the first work that derives convergence results for nonconvex optimization under arbitrary communication compression.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge