Nash Equilibrium Constrained Auto-bidding With Bi-level Reinforcement Learning
Paper and Code
Mar 13, 2025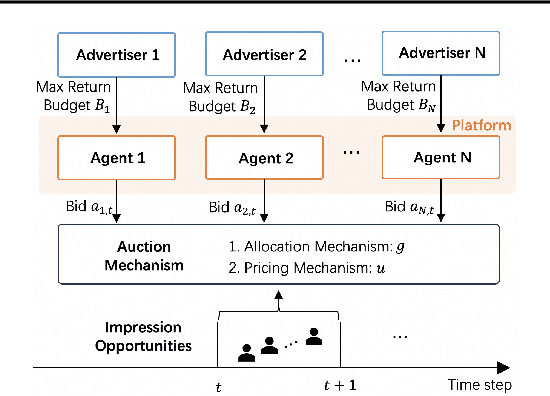
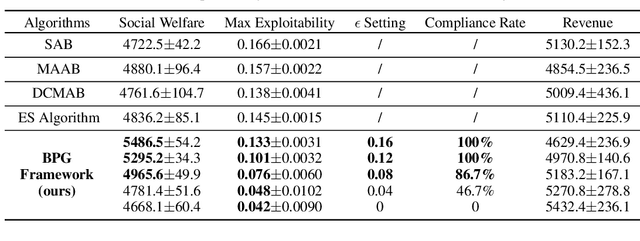


Many online advertising platforms provide advertisers with auto-bidding services to enhance their advertising performance. However, most existing auto-bidding algorithms fail to accurately capture the auto-bidding problem formulation that the platform truly faces, let alone solve it. Actually, we argue that the platform should try to help optimize each advertiser's performance to the greatest extent -- which makes $\epsilon$-Nash Equilibrium ($\epsilon$-NE) a necessary solution concept -- while maximizing the social welfare of all the advertisers for the platform's long-term value. Based on this, we introduce the \emph{Nash-Equilibrium Constrained Bidding} (NCB), a new formulation of the auto-bidding problem from the platform's perspective. Specifically, it aims to maximize the social welfare of all advertisers under the $\epsilon$-NE constraint. However, the NCB problem presents significant challenges due to its constrained bi-level structure and the typically large number of advertisers involved. To address these challenges, we propose a \emph{Bi-level Policy Gradient} (BPG) framework with theoretical guarantees. Notably, its computational complexity is independent of the number of advertisers, and the associated gradients are straightforward to compute. Extensive simulated and real-world experiments validate the effectiveness of the BPG framework.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge