Multitask Bandit Learning through Heterogeneous Feedback Aggregation

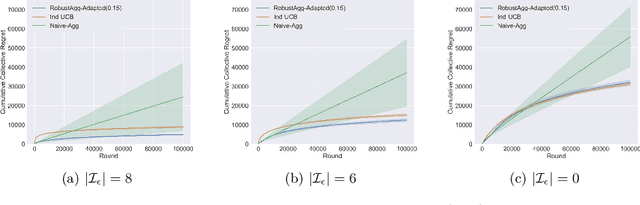
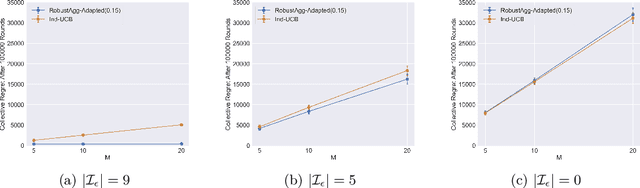
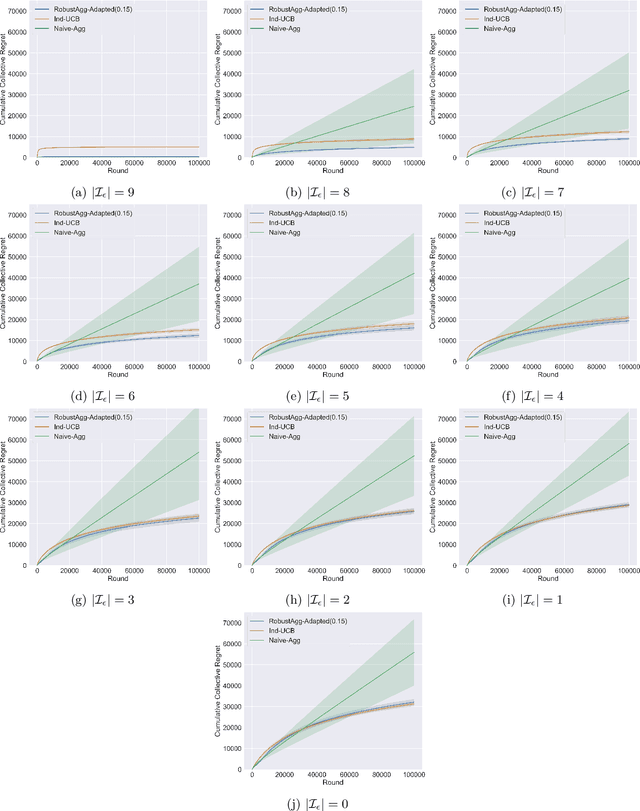
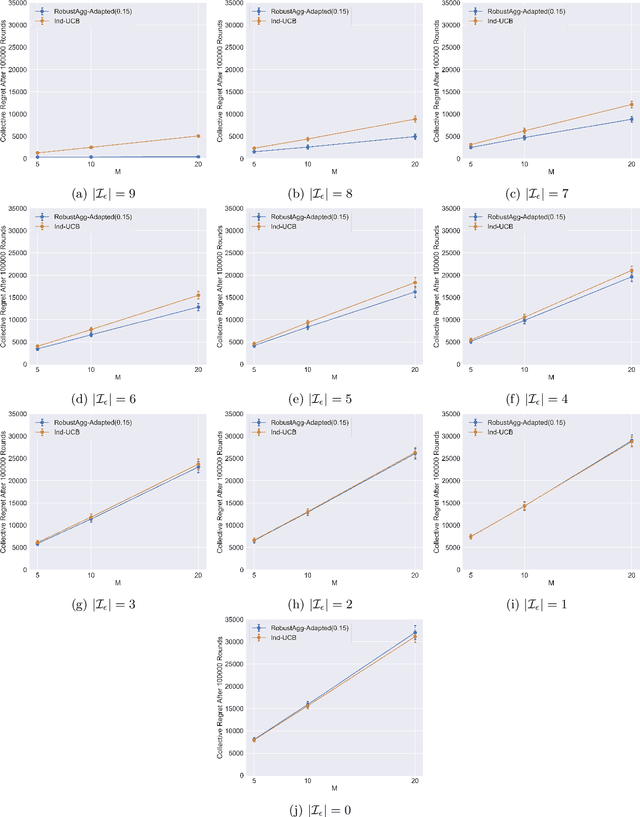
In many real-world applications, multiple agents seek to learn how to perform highly related yet slightly different tasks in an online bandit learning protocol. We formulate this problem as the $\epsilon$-multi-player multi-armed bandit problem, in which a set of players concurrently interact with a set of arms, and for each arm, the reward distributions for all players are similar but not necessarily identical. We develop an upper confidence bound-based algorithm, RobustAgg$(\epsilon)$, that adaptively aggregates rewards collected by different players. In the setting where an upper bound on the pairwise similarities of reward distributions between players is known, we achieve instance-dependent regret guarantees that depend on the amenability of information sharing across players. We complement these upper bounds with nearly matching lower bounds. In the setting where pairwise similarities are unknown, we provide a lower bound, as well as an algorithm that trades off minimax regret guarantees for adaptivity to unknown similarity structure.