Multinomial Random Forests: Fill the Gap between Theoretical Consistency and Empirical Soundness

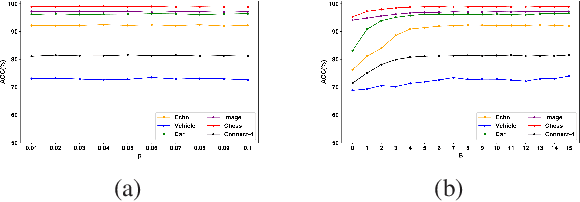
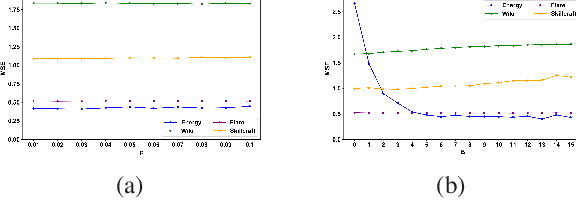
Random forests (RF) are one of the most widely used ensemble learning methods in classification and regression tasks. Despite its impressive performance, its theoretical consistency, which would ensure that its result converges to the optimum as the sample size increases, has been left far behind. Several consistent random forest variants have been proposed, yet all with relatively poor performance compared to the original random forests. In this paper, a novel RF framework named multinomial random forests (MRF) is proposed. In the MRF, an impurity-based multinomial distribution is constructed as the basis for the selection of a splitting point. This ensures that a certain degree of randomness is achieved while the overall quality of the trees is not much different from the original random forests. We prove the consistency of the MRF and demonstrate with multiple datasets that it performs similarly as the original random forests and better than existent consistent random forest variants for both classification and regression tasks.