Multi-Resolution Active Learning of Fourier Neural Operators

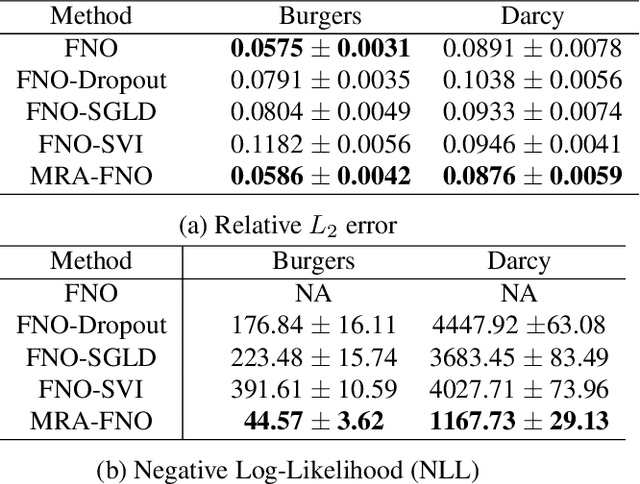
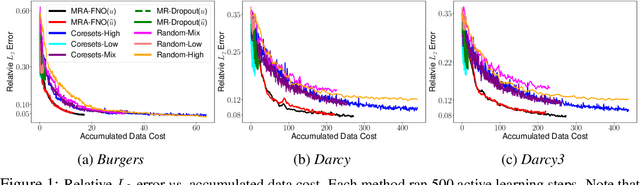
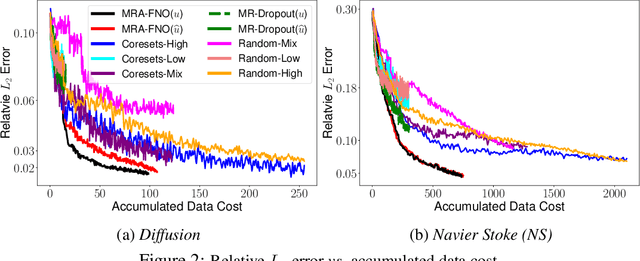
Fourier Neural Operator (FNO) is a popular operator learning framework, which not only achieves the state-of-the-art performance in many tasks, but also is highly efficient in training and prediction. However, collecting training data for the FNO is a costly bottleneck in practice, because it often demands expensive physical simulations. To overcome this problem, we propose Multi-Resolution Active learning of FNO (MRA-FNO), which can dynamically select the input functions and resolutions to lower the data cost as much as possible while optimizing the learning efficiency. Specifically, we propose a probabilistic multi-resolution FNO and use ensemble Monte-Carlo to develop an effective posterior inference algorithm. To conduct active learning, we maximize a utility-cost ratio as the acquisition function to acquire new examples and resolutions at each step. We use moment matching and the matrix determinant lemma to enable tractable, efficient utility computation. Furthermore, we develop a cost annealing framework to avoid over-penalizing high-resolution queries at the early stage. The over-penalization is severe when the cost difference is significant between the resolutions, which renders active learning often stuck at low-resolution queries and inferior performance. Our method overcomes this problem and applies to general multi-fidelity active learning and optimization problems. We have shown the advantage of our method in several benchmark operator learning tasks.