Mitigating Label Noise on Graph via Topological Sample Selection
Paper and Code
Mar 04, 2024
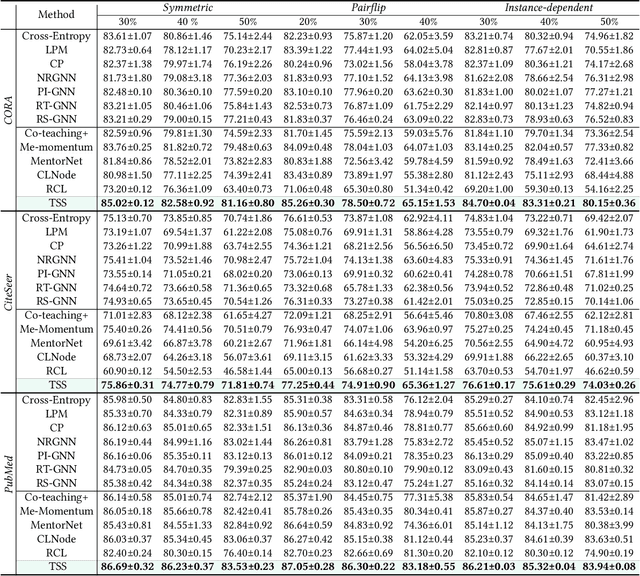


Despite the success of the carefully-annotated benchmarks, the effectiveness of existing graph neural networks (GNNs) can be considerably impaired in practice when the real-world graph data is noisily labeled. Previous explorations in sample selection have been demonstrated as an effective way for robust learning with noisy labels, however, the conventional studies focus on i.i.d data, and when moving to non-iid graph data and GNNs, two notable challenges remain: (1) nodes located near topological class boundaries are very informative for classification but cannot be successfully distinguished by the heuristic sample selection. (2) there is no available measure that considers the graph topological information to promote sample selection in a graph. To address this dilemma, we propose a $\textit{Topological Sample Selection}$ (TSS) method that boosts the informative sample selection process in a graph by utilising topological information. We theoretically prove that our procedure minimizes an upper bound of the expected risk under target clean distribution, and experimentally show the superiority of our method compared with state-of-the-art baselines.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge