Meta-Learning via Learned Loss

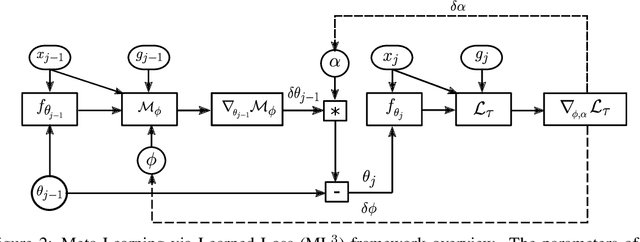
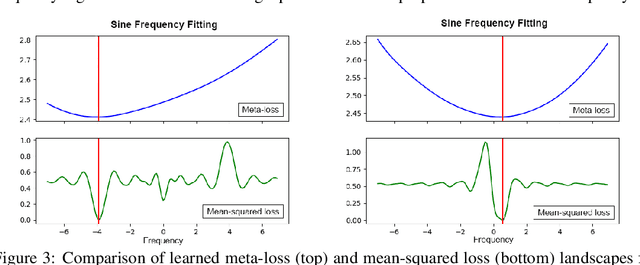
We present a meta-learning approach based on learning an adaptive, high-dimensional loss function that can generalize across multiple tasks and different model architectures. We develop a fully differentiable pipeline for learning a loss function targeted at maximizing the performance of an optimizee trained using this loss function. We observe that the loss landscape produced by our learned loss significantly improves upon the original task-specific loss. We evaluate our method on supervised and reinforcement learning tasks. Furthermore, we show that our pipeline is able to operate in sparse reward and self-supervised reinforcement learning scenarios.