Memory In Memory: A Predictive Neural Network for Learning Higher-Order Non-Stationarity from Spatiotemporal Dynamics

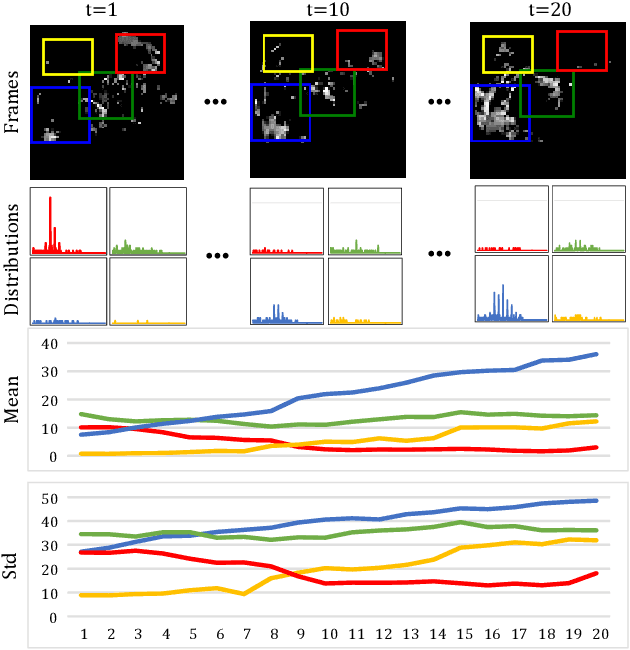
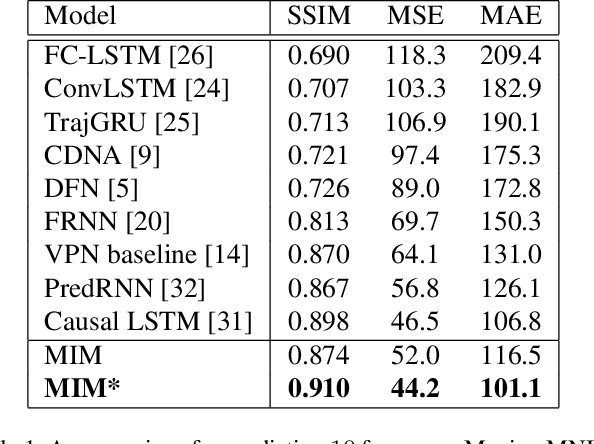
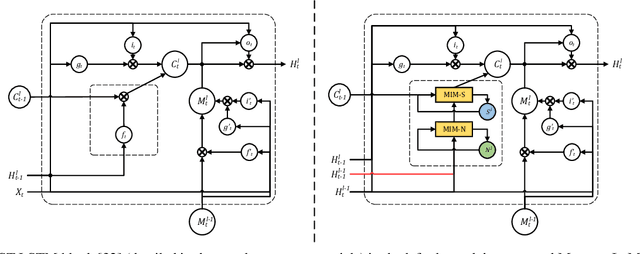
Natural spatiotemporal processes can be highly non-stationary in many ways, e.g. the low-level non-stationarity such as spatial correlations or temporal dependencies of local pixel values; and the high-level variations such as the accumulation, deformation or dissipation of radar echoes in precipitation forecasting. From Cramer's Decomposition, any non-stationary process can be decomposed into deterministic, time-variant polynomials, plus a zero-mean stochastic term. By applying differencing operations appropriately, we may turn time-variant polynomials into a constant, making the deterministic component predictable. However, most previous recurrent neural networks for spatiotemporal prediction do not use the differential signals effectively, and their relatively simple state transition functions prevent them from learning too complicated variations in spacetime. We propose the Memory In Memory (MIM) networks and corresponding recurrent blocks for this purpose. The MIM blocks exploit the differential signals between adjacent recurrent states to model the non-stationary and approximately stationary properties in spatiotemporal dynamics with two cascaded, self-renewed memory modules. By stacking multiple MIM blocks, we could potentially handle higher-order non-stationarity. The MIM networks achieve the state-of-the-art results on three spatiotemporal prediction tasks across both synthetic and real-world datasets. We believe that the general idea of this work can be potentially applied to other time-series forecasting tasks.