MaxMatch: Semi-Supervised Learning with Worst-Case Consistency
Paper and Code
Sep 26, 2022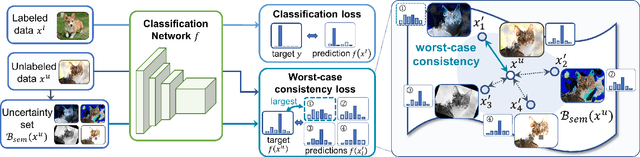
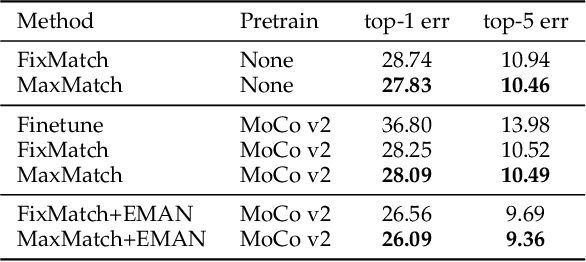

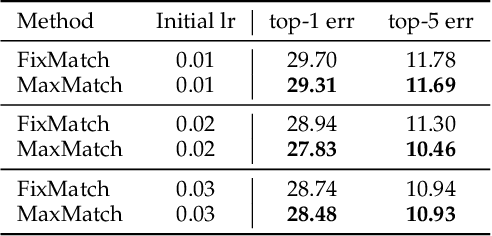
In recent years, great progress has been made to incorporate unlabeled data to overcome the inefficiently supervised problem via semi-supervised learning (SSL). Most state-of-the-art models are based on the idea of pursuing consistent model predictions over unlabeled data toward the input noise, which is called consistency regularization. Nonetheless, there is a lack of theoretical insights into the reason behind its success. To bridge the gap between theoretical and practical results, we propose a worst-case consistency regularization technique for SSL in this paper. Specifically, we first present a generalization bound for SSL consisting of the empirical loss terms observed on labeled and unlabeled training data separately. Motivated by this bound, we derive an SSL objective that minimizes the largest inconsistency between an original unlabeled sample and its multiple augmented variants. We then provide a simple but effective algorithm to solve the proposed minimax problem, and theoretically prove that it converges to a stationary point. Experiments on five popular benchmark datasets validate the effectiveness of our proposed method.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge