Low-variance estimation in the Plackett-Luce model via quasi-Monte Carlo sampling
Paper and Code
May 12, 2022
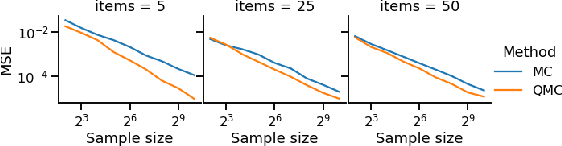
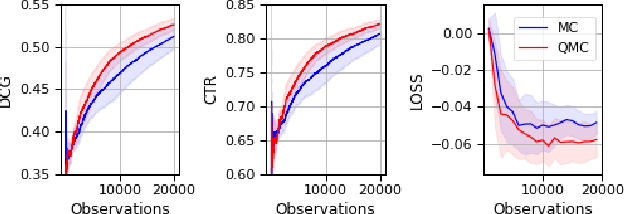

The Plackett-Luce (PL) model is ubiquitous in learning-to-rank (LTR) because it provides a useful and intuitive probabilistic model for sampling ranked lists. Counterfactual offline evaluation and optimization of ranking metrics are pivotal for using LTR methods in production. When adopting the PL model as a ranking policy, both tasks require the computation of expectations with respect to the model. These are usually approximated via Monte-Carlo (MC) sampling, since the combinatorial scaling in the number of items to be ranked makes their analytical computation intractable. Despite recent advances in improving the computational efficiency of the sampling process via the Gumbel top-k trick, the MC estimates can suffer from high variance. We develop a novel approach to producing more sample-efficient estimators of expectations in the PL model by combining the Gumbel top-k trick with quasi-Monte Carlo (QMC) sampling, a well-established technique for variance reduction. We illustrate our findings both theoretically and empirically using real-world recommendation data from Amazon Music and the Yahoo learning-to-rank challenge.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge