Logical Satisfiability of Counterfactuals for Faithful Explanations in NLI
Paper and Code
May 25, 2022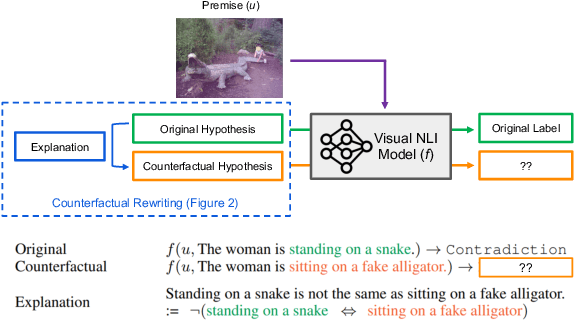


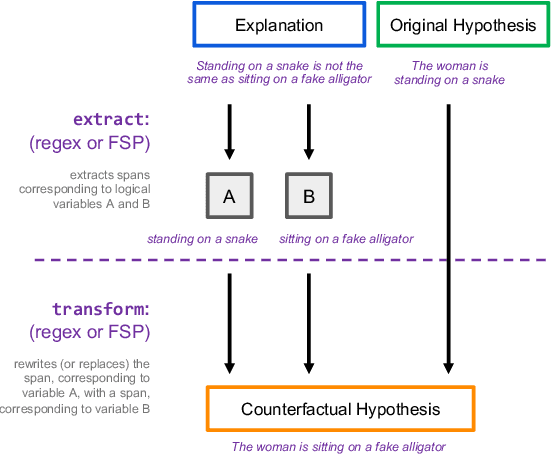
Evaluating an explanation's faithfulness is desired for many reasons such as trust, interpretability and diagnosing the sources of model's errors. In this work, which focuses on the NLI task, we introduce the methodology of Faithfulness-through-Counterfactuals, which first generates a counterfactual hypothesis based on the logical predicates expressed in the explanation, and then evaluates if the model's prediction on the counterfactual is consistent with that expressed logic (i.e. if the new formula is \textit{logically satisfiable}). In contrast to existing approaches, this does not require any explanations for training a separate verification model. We first validate the efficacy of automatic counterfactual hypothesis generation, leveraging on the few-shot priming paradigm. Next, we show that our proposed metric distinguishes between human-model agreement and disagreement on new counterfactual input. In addition, we conduct a sensitivity analysis to validate that our metric is sensitive to unfaithful explanations.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge