Localized LRR on Grassmann Manifolds: An Extrinsic View
Paper and Code
May 17, 2017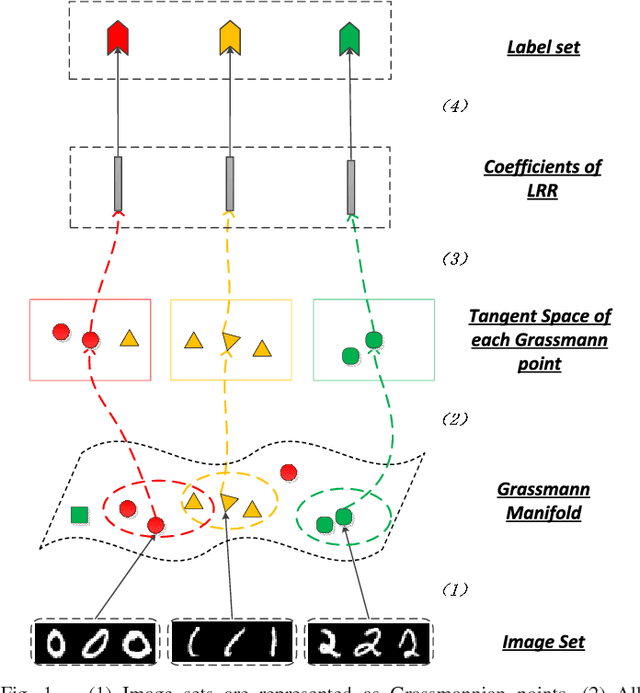


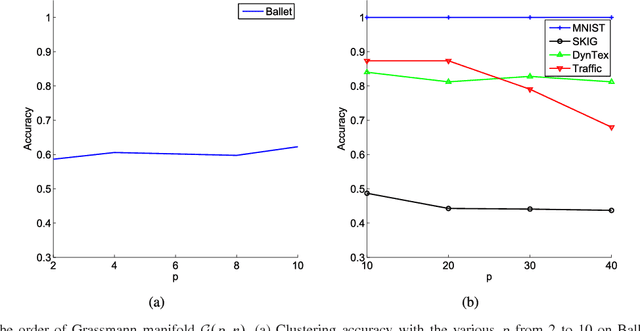
Subspace data representation has recently become a common practice in many computer vision tasks. It demands generalizing classical machine learning algorithms for subspace data. Low-Rank Representation (LRR) is one of the most successful models for clustering vectorial data according to their subspace structures. This paper explores the possibility of extending LRR for subspace data on Grassmann manifolds. Rather than directly embedding the Grassmann manifolds into the symmetric matrix space, an extrinsic view is taken to build the LRR self-representation in the local area of the tangent space at each Grassmannian point, resulting in a localized LRR method on Grassmann manifolds. A novel algorithm for solving the proposed model is investigated and implemented. The performance of the new clustering algorithm is assessed through experiments on several real-world datasets including MNIST handwritten digits, ballet video clips, SKIG action clips, DynTex++ dataset and highway traffic video clips. The experimental results show the new method outperforms a number of state-of-the-art clustering methods
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge