Linear Connectivity Reveals Generalization Strategies
Paper and Code
May 24, 2022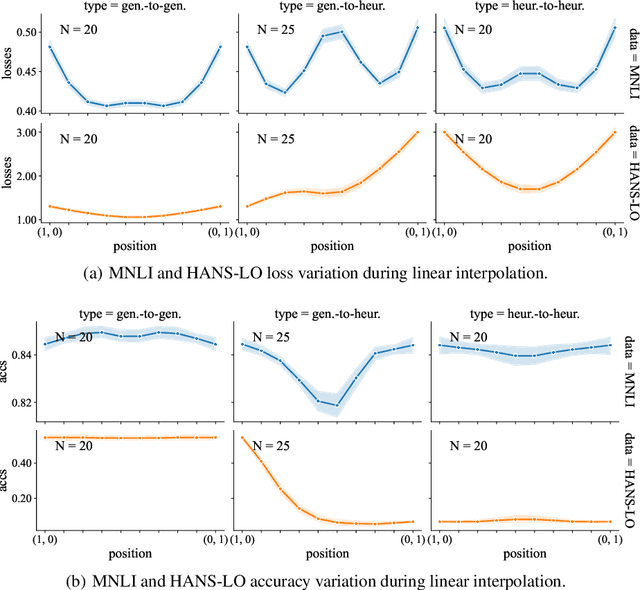
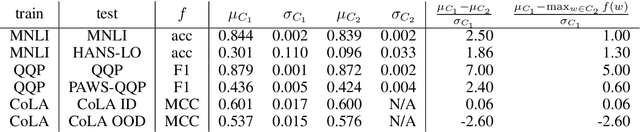
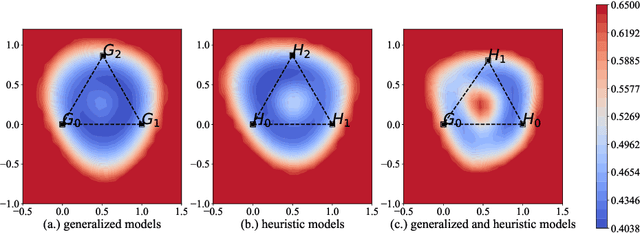
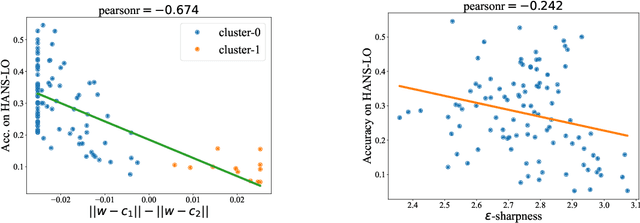
It is widely accepted in the mode connectivity literature that when two neural networks are trained similarly on the same data, they are connected by a path through parameter space over which test set accuracy is maintained. Under some circumstances, including transfer learning from pretrained models, these paths are presumed to be linear. In contrast to existing results, we find that among text classifiers (trained on MNLI, QQP, and CoLA), some pairs of finetuned models have large barriers of increasing loss on the linear paths between them. On each task, we find distinct clusters of models which are linearly connected on the test loss surface, but are disconnected from models outside the cluster -- models that occupy separate basins on the surface. By measuring performance on specially-crafted diagnostic datasets, we find that these clusters correspond to different generalization strategies: one cluster behaves like a bag of words model under domain shift, while another cluster uses syntactic heuristics. Our work demonstrates how the geometry of the loss surface can guide models towards different heuristic functions.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge