Learning to Refit for Convex Learning Problems
Paper and Code
Nov 24, 2021


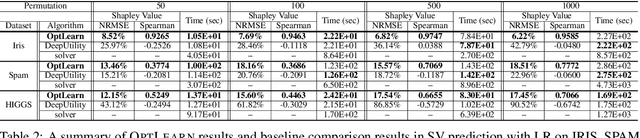
Machine learning (ML) models need to be frequently retrained on changing datasets in a wide variety of application scenarios, including data valuation and uncertainty quantification. To efficiently retrain the model, linear approximation methods such as influence function have been proposed to estimate the impact of data changes on model parameters. However, these methods become inaccurate for large dataset changes. In this work, we focus on convex learning problems and propose a general framework to learn to estimate optimized model parameters for different training sets using neural networks. We propose to enforce the predicted model parameters to obey optimality conditions and maintain utility through regularization techniques, which significantly improve generalization. Moreover, we rigorously characterize the expressive power of neural networks to approximate the optimizer of convex problems. Empirical results demonstrate the advantage of the proposed method in accurate and efficient model parameter estimation compared to the state-of-the-art.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge