Learning to Fuse Local Geometric Features for 3D Rigid Data Matching
Paper and Code
Apr 27, 2019
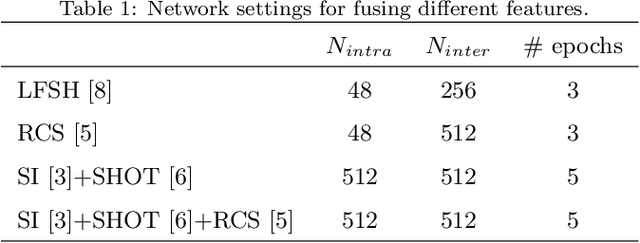
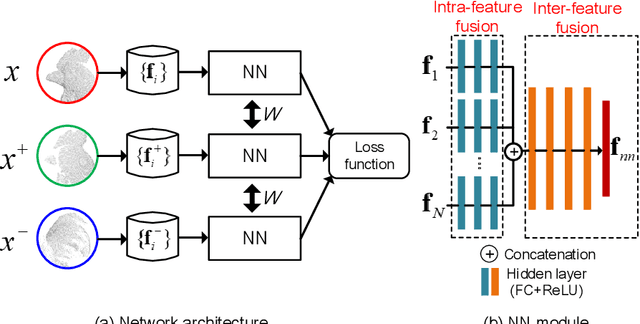
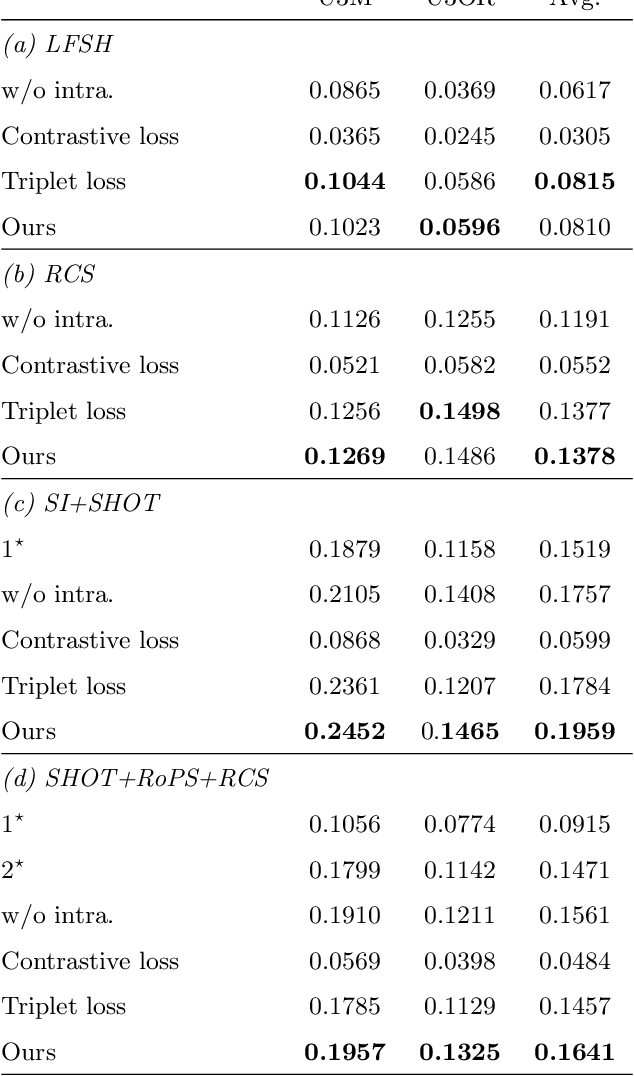
This paper presents a simple yet very effective data-driven approach to fuse both low-level and high-level local geometric features for 3D rigid data matching. It is a common practice to generate distinctive geometric descriptors by fusing low-level features from various viewpoints or subspaces, or enhance geometric feature matching by leveraging multiple high-level features. In prior works, they are typically performed via linear operations such as concatenation and min pooling. We show that more compact and distinctive representations can be achieved by optimizing a neural network (NN) model under the triplet framework that non-linearly fuses local geometric features in Euclidean spaces. The NN model is trained by an improved triplet loss function that fully leverages all pairwise relationships within the triplet. Moreover, the fused descriptor by our approach is also competitive to deep learned descriptors from raw data while being more lightweight and rotational invariant. Experimental results on four standard datasets with various data modalities and application contexts confirm the advantages of our approach in terms of both feature matching and geometric registration.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge