Learning Probabilistic Coordinate Fields for Robust Correspondences
Paper and Code
Jun 07, 2023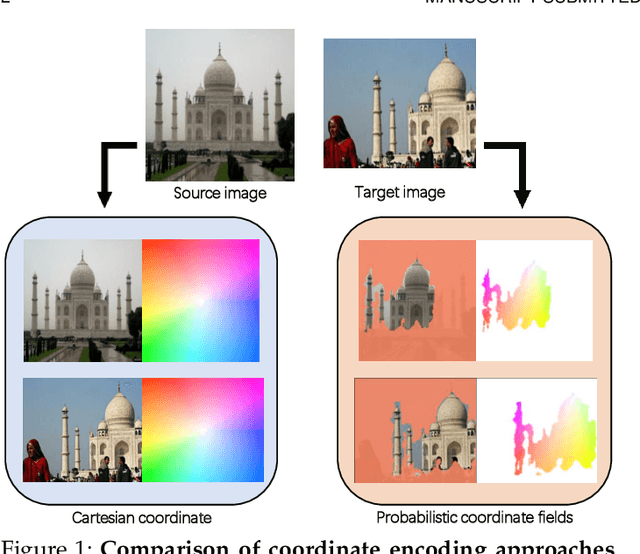


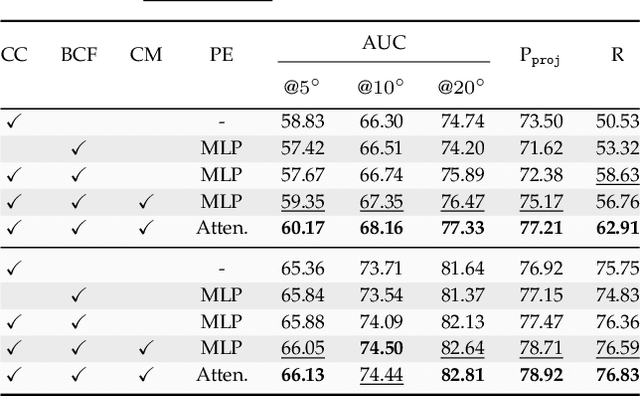
We introduce Probabilistic Coordinate Fields (PCFs), a novel geometric-invariant coordinate representation for image correspondence problems. In contrast to standard Cartesian coordinates, PCFs encode coordinates in correspondence-specific barycentric coordinate systems (BCS) with affine invariance. To know \textit{when and where to trust} the encoded coordinates, we implement PCFs in a probabilistic network termed PCF-Net, which parameterizes the distribution of coordinate fields as Gaussian mixture models. By jointly optimizing coordinate fields and their confidence conditioned on dense flows, PCF-Net can work with various feature descriptors when quantifying the reliability of PCFs by confidence maps. An interesting observation of this work is that the learned confidence map converges to geometrically coherent and semantically consistent regions, which facilitates robust coordinate representation. By delivering the confident coordinates to keypoint/feature descriptors, we show that PCF-Net can be used as a plug-in to existing correspondence-dependent approaches. Extensive experiments on both indoor and outdoor datasets suggest that accurate geometric invariant coordinates help to achieve the state of the art in several correspondence problems, such as sparse feature matching, dense image registration, camera pose estimation, and consistency filtering. Further, the interpretable confidence map predicted by PCF-Net can also be leveraged to other novel applications from texture transfer to multi-homography classification.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge