Learning Node Representations from Noisy Graph Structures
Paper and Code
Dec 04, 2020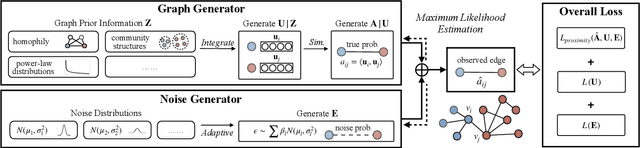
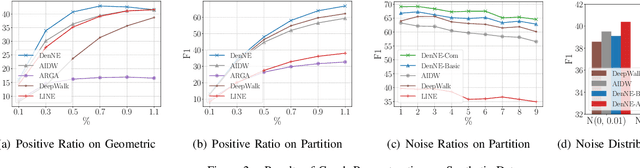
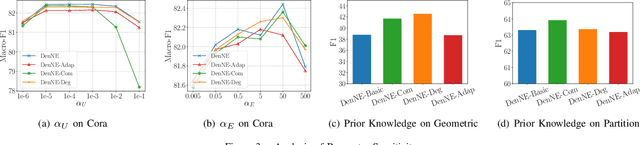
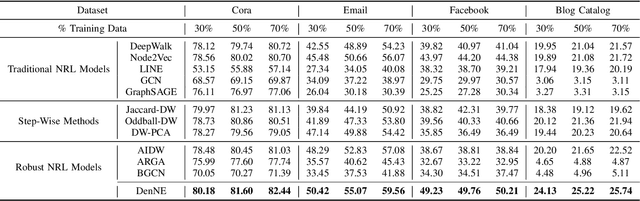
Learning low-dimensional representations on graphs has proved to be effective in various downstream tasks. However, noises prevail in real-world networks, which compromise networks to a large extent in that edges in networks propagate noises through the whole network instead of only the node itself. While existing methods tend to focus on preserving structural properties, the robustness of the learned representations against noises is generally ignored. In this paper, we propose a novel framework to learn noise-free node representations and eliminate noises simultaneously. Since noises are often unknown on real graphs, we design two generators, namely a graph generator and a noise generator, to identify normal structures and noises in an unsupervised setting. On the one hand, the graph generator serves as a unified scheme to incorporate any useful graph prior knowledge to generate normal structures. We illustrate the generative process with community structures and power-law degree distributions as examples. On the other hand, the noise generator generates graph noises not only satisfying some fundamental properties but also in an adaptive way. Thus, real noises with arbitrary distributions can be handled successfully. Finally, in order to eliminate noises and obtain noise-free node representations, two generators need to be optimized jointly, and through maximum likelihood estimation, we equivalently convert the model into imposing different regularization constraints on the true graph and noises respectively. Our model is evaluated on both real-world and synthetic data. It outperforms other strong baselines for node classification and graph reconstruction tasks, demonstrating its ability to eliminate graph noises.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge