Learning Differential Operators for Interpretable Time Series Modeling
Paper and Code
Sep 03, 2022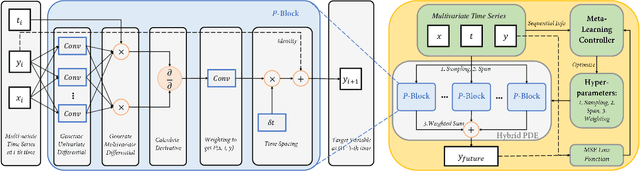


Modeling sequential patterns from data is at the core of various time series forecasting tasks. Deep learning models have greatly outperformed many traditional models, but these black-box models generally lack explainability in prediction and decision making. To reveal the underlying trend with understandable mathematical expressions, scientists and economists tend to use partial differential equations (PDEs) to explain the highly nonlinear dynamics of sequential patterns. However, it usually requires domain expert knowledge and a series of simplified assumptions, which is not always practical and can deviate from the ever-changing world. Is it possible to learn the differential relations from data dynamically to explain the time-evolving dynamics? In this work, we propose an learning framework that can automatically obtain interpretable PDE models from sequential data. Particularly, this framework is comprised of learnable differential blocks, named $P$-blocks, which is proved to be able to approximate any time-evolving complex continuous functions in theory. Moreover, to capture the dynamics shift, this framework introduces a meta-learning controller to dynamically optimize the hyper-parameters of a hybrid PDE model. Extensive experiments on times series forecasting of financial, engineering, and health data show that our model can provide valuable interpretability and achieve comparable performance to state-of-the-art models. From empirical studies, we find that learning a few differential operators may capture the major trend of sequential dynamics without massive computational complexity.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge