Joint Coreset Construction and Quantization for Distributed Machine Learning
Paper and Code
Apr 13, 2022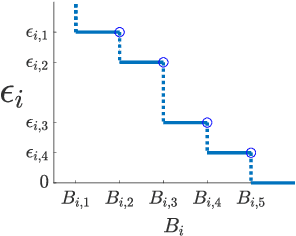
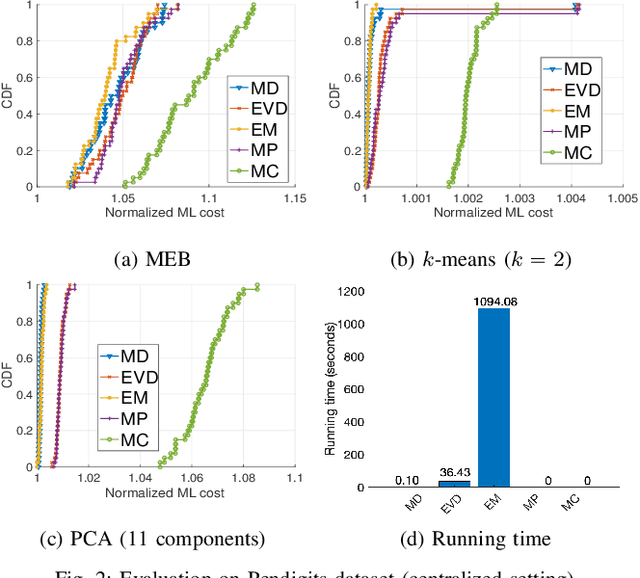
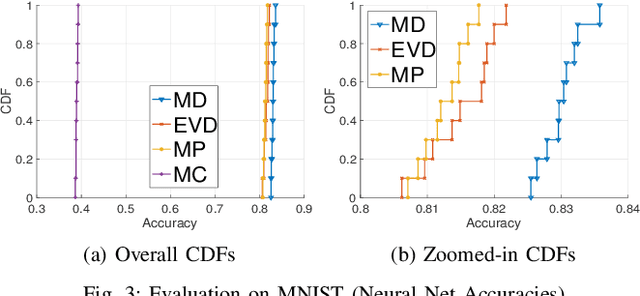
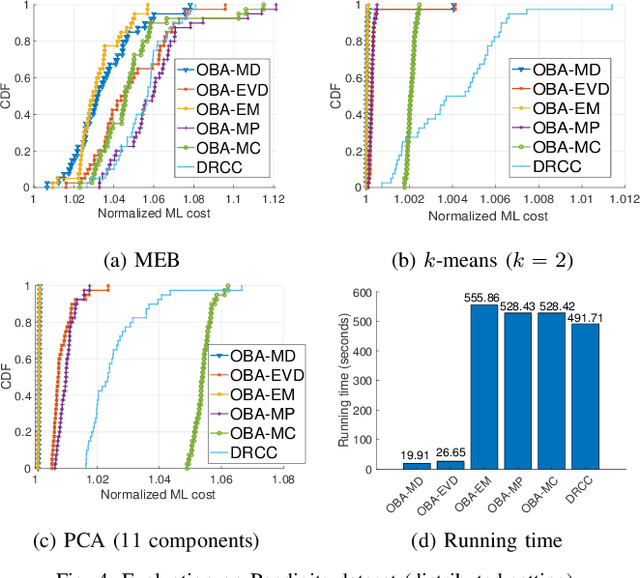
Coresets are small, weighted summaries of larger datasets, aiming at providing provable error bounds for machine learning (ML) tasks while significantly reducing the communication and computation costs. To achieve a better trade-off between ML error bounds and costs, we propose the first framework to incorporate quantization techniques into the process of coreset construction. Specifically, we theoretically analyze the ML error bounds caused by a combination of coreset construction and quantization. Based on that, we formulate an optimization problem to minimize the ML error under a fixed budget of communication cost. To improve the scalability for large datasets, we identify two proxies of the original objective function, for which efficient algorithms are developed. For the case of data on multiple nodes, we further design a novel algorithm to allocate the communication budget to the nodes while minimizing the overall ML error. Through extensive experiments on multiple real-world datasets, we demonstrate the effectiveness and efficiency of our proposed algorithms for a variety of ML tasks. In particular, our algorithms have achieved more than 90% data reduction with less than 10% degradation in ML performance in most cases.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge