Joint Contrastive Learning for Unsupervised Domain Adaptation
Paper and Code
Jun 18, 2020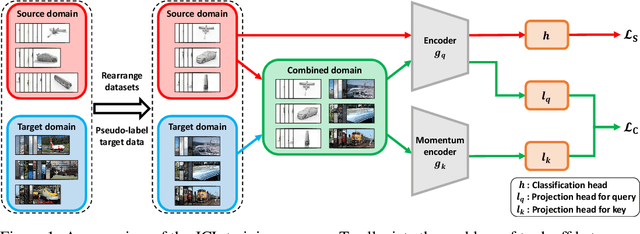
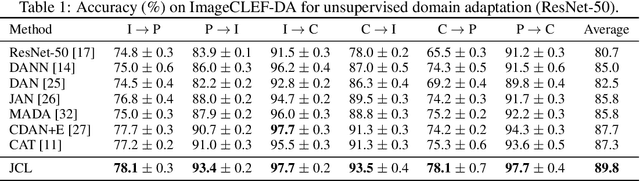
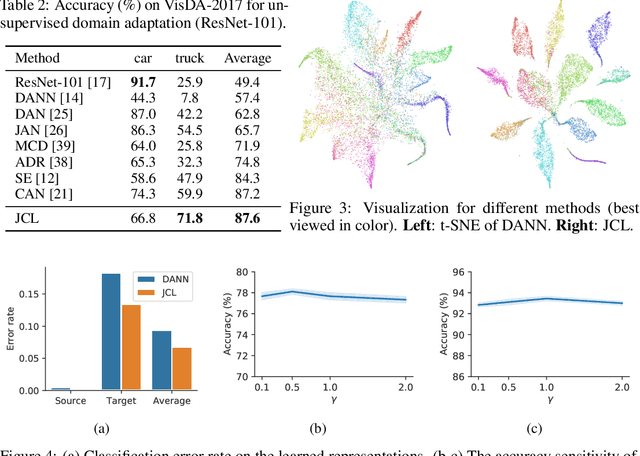

Enhancing feature transferability by matching marginal distributions has led to improvements in domain adaptation, although this is at the expense of feature discrimination. In particular, the ideal joint hypothesis error in the target error upper bound, which was previously considered to be minute, has been found to be significant, impairing its theoretical guarantee. In this paper, we propose an alternative upper bound on the target error that explicitly considers the joint error to render it more manageable. With the theoretical analysis, we suggest a joint optimization framework that combines the source and target domains. Further, we introduce Joint Contrastive Learning (JCL) to find class-level discriminative features, which is essential for minimizing the joint error. With a solid theoretical framework, JCL employs contrastive loss to maximize the mutual information between a feature and its label, which is equivalent to maximizing the Jensen-Shannon divergence between conditional distributions. Experiments on two real-world datasets demonstrate that JCL outperforms the state-of-the-art methods.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge