Investigating Channel Pruning through Structural Redundancy Reduction - A Statistical Study

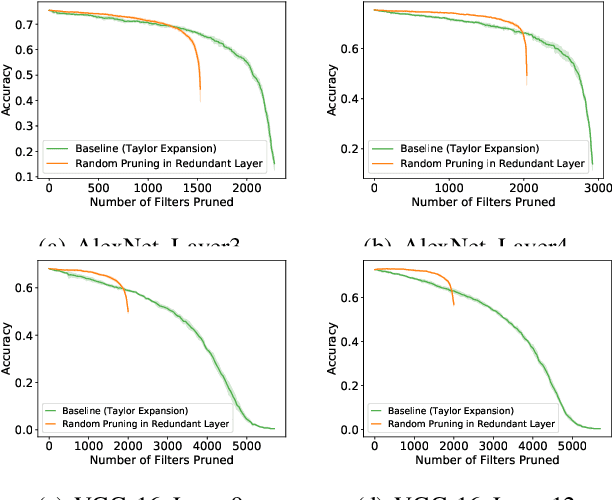
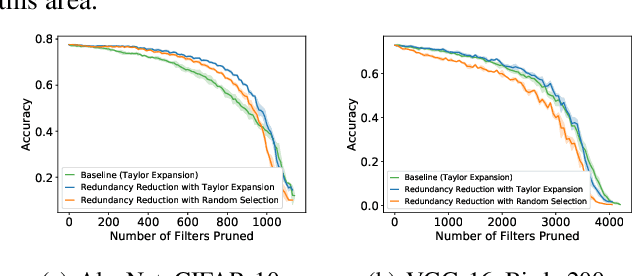
Most existing channel pruning methods formulate the pruning task from a perspective of inefficiency reduction which iteratively rank and remove the least important filters, or find the set of filters that minimizes some reconstruction errors after pruning. In this work, we investigate the channel pruning from a new perspective with statistical modeling. We hypothesize that the number of filters at a certain layer reflects the level of 'redundancy' in that layer and thus formulate the pruning problem from the aspect of redundancy reduction. Based on both theoretic analysis and empirical studies, we make an important discovery: randomly pruning filters from layers of high redundancy outperforms pruning the least important filters across all layers based on the state-of-the-art ranking criterion. These results advance our understanding of pruning and further testify to the recent findings that the structure of the pruned model plays a key role in the network efficiency as compared to inherited weights.