Invariant Adversarial Learning for Distributional Robustness

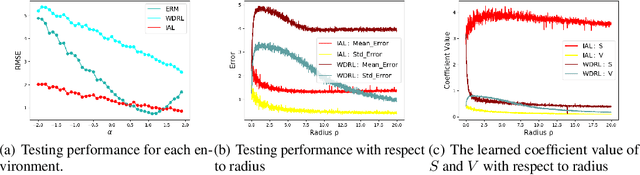
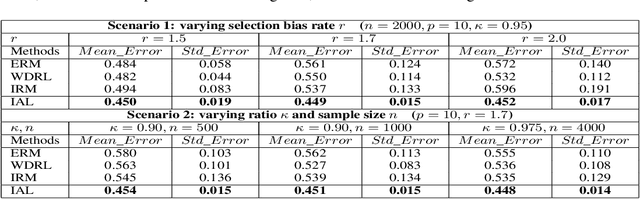
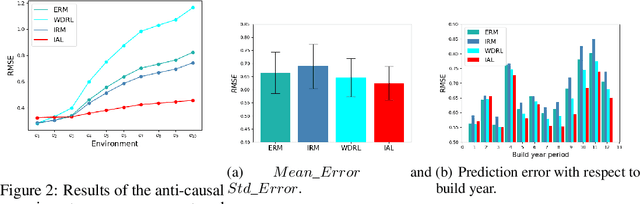
Machine learning algorithms with empirical risk minimization are vulnerable to distributional shifts due to the greedy adoption of all the correlations found in training data. Recently, there are robust learning methods aiming at this problem by minimizing the worst-case risk over an uncertainty set. However, they equally treat all covariates to form the uncertainty sets regardless of the stability of their correlations with the target, resulting in the overwhelmingly large set and low confidence of the learner. In this paper, we propose the Invariant Adversarial Learning (IAL) algorithm that leverages heterogeneous data sources to construct a more practical uncertainty set and conduct robustness optimization, where covariates are differentiated according to the stability of their correlations with the target. We theoretically show that our method is tractable for stochastic gradient-based optimization and provide the performance guarantees for our method. Empirical studies on both simulation and real datasets validate the effectiveness of our method in terms of robust performance across unknown distributional shifts.