Intra Order-preserving Functions for Calibration of Multi-Class Neural Networks
Paper and Code
Mar 15, 2020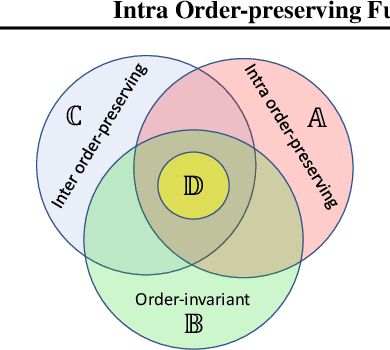

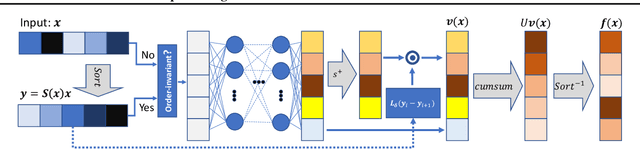

Predicting calibrated confidence scores for multi-class deep networks is important for avoiding rare but costly mistakes. A common approach is to learn a post-hoc calibration function that transforms the output of the original network into calibrated confidence scores while maintaining the network's accuracy. However, previous post-hoc calibration techniques work only with simple calibration functions, potentially lacking sufficient representation to calibrate the complex function landscape of deep networks. In this work, we aim to learn general post-hoc calibration functions that can preserve the top-k predictions of any deep network. We call this family of functions intra order-preserving functions. We propose a new neural network architecture that represents a class of intra order-preserving functions by combining common neural network components. Additionally, we introduce order-invariant and diagonal sub-families, which can act as regularization for better generalization when the training data size is small. We show the effectiveness of the proposed method across a wide range of datasets and classifiers. Our method outperforms state-of-the-art post-hoc calibration methods, namely temperature scaling and Dirichlet calibration, in multiple settings.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge