Interpretable-AI Policies using Evolutionary Nonlinear Decision Trees for Discrete Action Systems

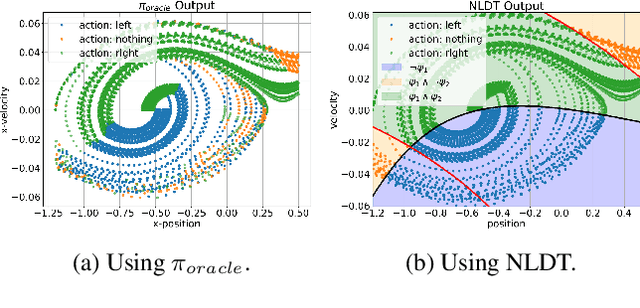
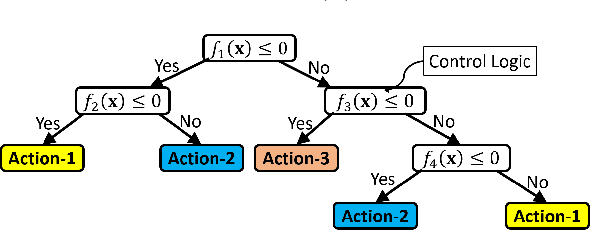
Black-box artificial intelligence (AI) induction methods such as deep reinforcement learning (DRL) are increasingly being used to find optimal policies for a given control task. Although policies represented using a black-box AI are capable of efficiently executing the underlying control task and achieving optimal closed-loop performance -- controlling the agent from initial time step until the successful termination of an episode, the developed control rules are often complex and neither interpretable nor explainable. In this paper, we use a recently proposed nonlinear decision-tree (NLDT) approach to find a hierarchical set of control rules in an attempt to maximize the open-loop performance for approximating and explaining the pre-trained black-box DRL (oracle) agent using the labelled state-action dataset. Recent advances in nonlinear optimization approaches using evolutionary computation facilitates finding a hierarchical set of nonlinear control rules as a function of state variables using a computationally fast bilevel optimization procedure at each node of the proposed NLDT. Additionally, we propose a re-optimization procedure for enhancing closed-loop performance of an already derived NLDT. We evaluate our proposed methodologies on four different control problems having two to four discrete actions. In all these problems our proposed approach is able to find simple and interpretable rules involving one to four non-linear terms per rule, while simultaneously achieving on par closed-loop performance when compared to a trained black-box DRL agent. The obtained results are inspiring as they suggest the replacement of complicated black-box DRL policies involving thousands of parameters (making them non-interpretable) with simple interpretable policies. Results are encouraging and motivating to pursue further applications of proposed approach in solving more complex control tasks.