Integrated Model, Batch and Domain Parallelism in Training Neural Networks
Paper and Code
May 16, 2018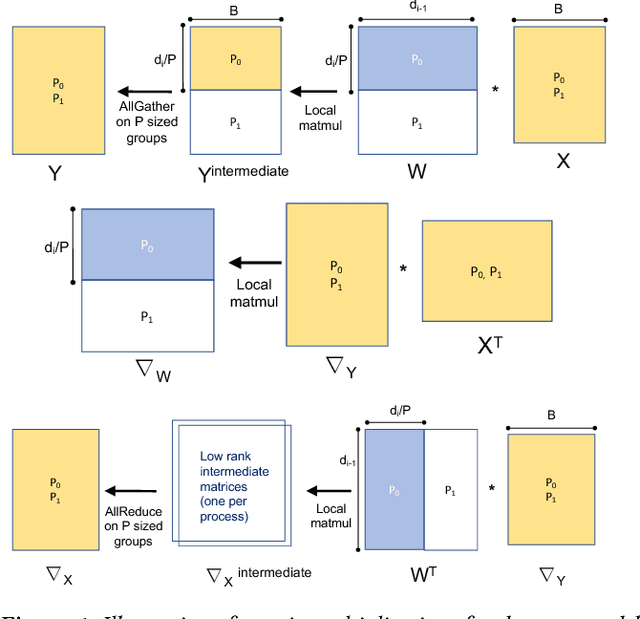
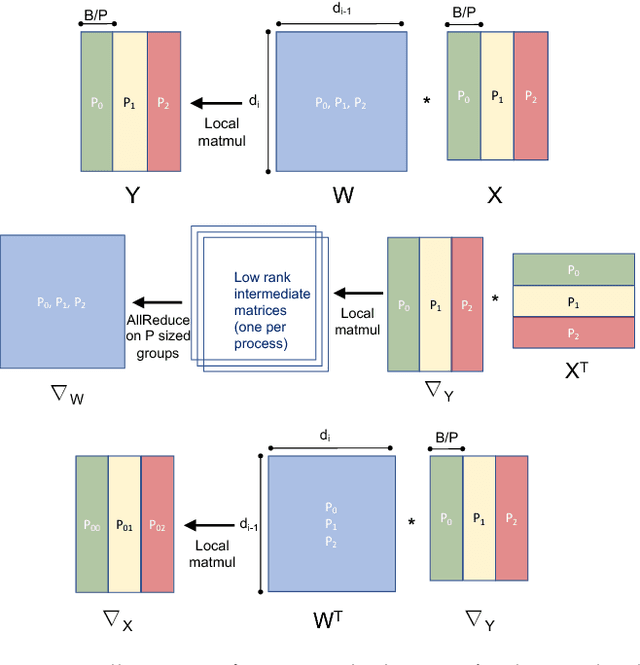

We propose a new integrated method of exploiting model, batch and domain parallelism for the training of deep neural networks (DNNs) on large distributed-memory computers using minibatch stochastic gradient descent (SGD). Our goal is to find an efficient parallelization strategy for a fixed batch size using $P$ processes. Our method is inspired by the communication-avoiding algorithms in numerical linear algebra. We see $P$ processes as logically divided into a $P_r \times P_c$ grid where the $P_r$ dimension is implicitly responsible for model/domain parallelism and the $P_c$ dimension is implicitly responsible for batch parallelism. In practice, the integrated matrix-based parallel algorithm encapsulates these types of parallelism automatically. We analyze the communication complexity and analytically demonstrate that the lowest communication costs are often achieved neither with pure model nor with pure data parallelism. We also show how the domain parallel approach can help in extending the theoretical scaling limit of the typical batch parallel method.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge