Initialization Matters: Regularizing Manifold-informed Initialization for Neural Recommendation Systems
Paper and Code
Jun 09, 2021

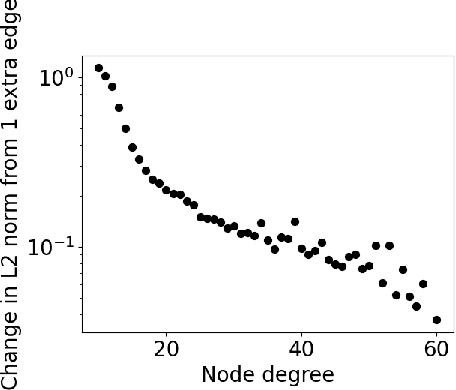
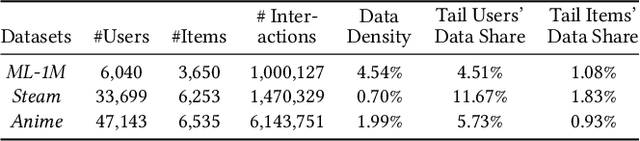
Proper initialization is crucial to the optimization and the generalization of neural networks. However, most existing neural recommendation systems initialize the user and item embeddings randomly. In this work, we propose a new initialization scheme for user and item embeddings called Laplacian Eigenmaps with Popularity-based Regularization for Isolated Data (LEPORID). LEPORID endows the embeddings with information regarding multi-scale neighborhood structures on the data manifold and performs adaptive regularization to compensate for high embedding variance on the tail of the data distribution. Exploiting matrix sparsity, LEPORID embeddings can be computed efficiently. We evaluate LEPORID in a wide range of neural recommendation models. In contrast to the recent surprising finding that the simple K-nearest-neighbor (KNN) method often outperforms neural recommendation systems, we show that existing neural systems initialized with LEPORID often perform on par or better than KNN. To maximize the effects of the initialization, we propose the Dual-Loss Residual Recommendation (DLR2) network, which, when initialized with LEPORID, substantially outperforms both traditional and state-of-the-art neural recommender systems.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge