Information-Guided Robotic Maximum Seek-and-Sample in Partially Observable Continuous Environments
Paper and Code
Sep 26, 2019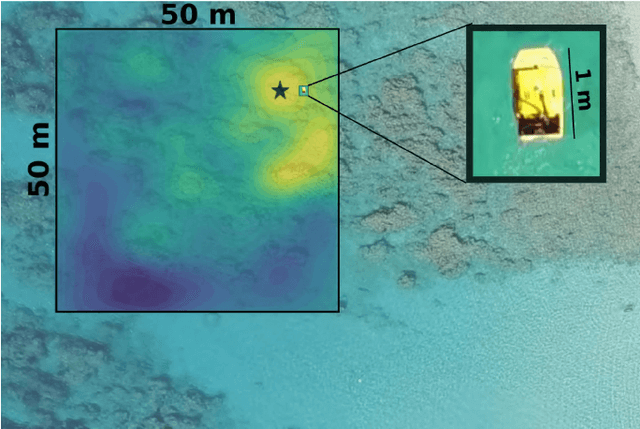
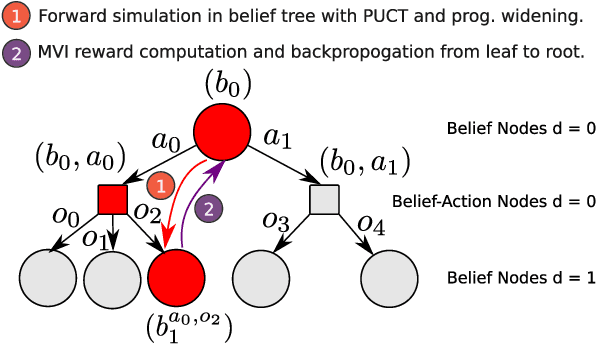
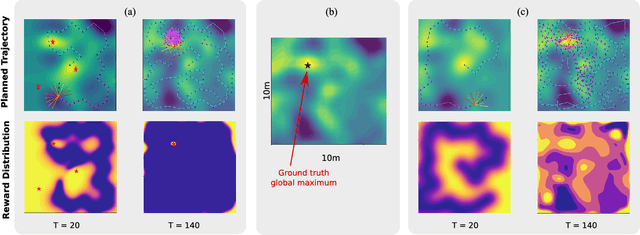
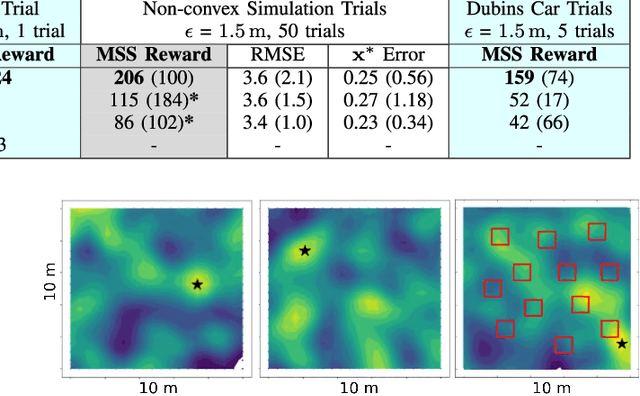
We present PLUMES, a planner to localizing and collecting samples at the global maximum of an a priori unknown and partially observable continuous environment. The "maximum-seek-and-sample" (MSS) problem is pervasive in the environmental and earth sciences. Experts want to collect scientifically valuable samples at an environmental maximum (e.g., an oil-spill source), but do not have prior knowledge about the phenomenon's distribution. We formulate the MSS problem as a partially-observable Markov decision process (POMDP) with continuous state and observation spaces, and a sparse reward signal. To solve the MSS POMDP, PLUMES uses an information-theoretic reward heuristic with continous-observation Monte Carlo Tree Search to efficiently localize and sample from the global maximum. In simulation and field experiments, PLUMES collects more scientifically valuable samples than state-of-the-art planners in a diverse set of environments, with various platforms, sensors, and challenging real-world conditions.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge