Inferring Multi-Dimensional Rates of Aging from Cross-Sectional Data
Paper and Code
Jul 12, 2018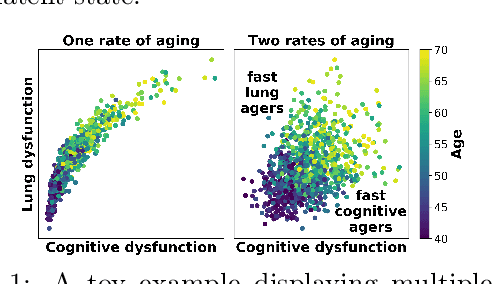
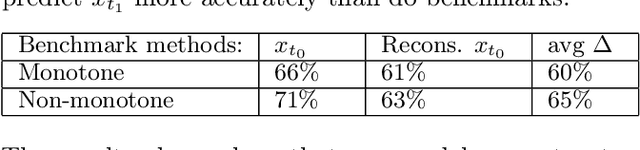
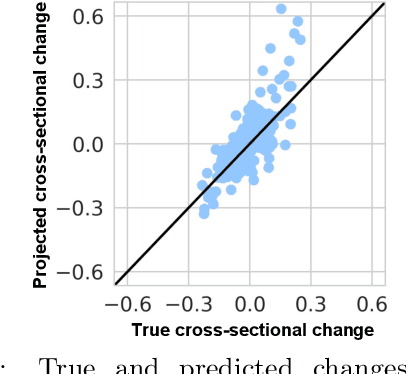
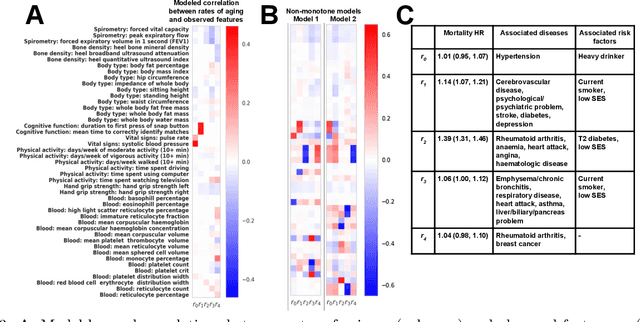
Modeling how individuals evolve over time is a fundamental problem in the natural and social sciences. However, existing datasets are often cross-sectional with each individual only observed at a single timepoint, making inference of temporal dynamics hard. Motivated by the study of human aging, we present a model that can learn temporal dynamics from cross-sectional data. Our model represents each individual with a low-dimensional latent state that consists of 1) a dynamic vector $rt$ that evolves linearly with time $t$, where $r$ is an individual-specific "rate of aging" vector, and 2) a static vector $b$ that captures time-independent variation. Observed features are a non-linear function of $rt$ and $b$. We prove that constraining the mapping between $rt$ and a subset of the observed features to be order-isomorphic yields a model class that is identifiable if the distribution of time-independent variation is known. Our model correctly recovers the latent rate vector $r$ in realistic synthetic data. Applied to the UK Biobank human health dataset, our model accurately reconstructs the observed data while learning interpretable rates of aging $r$ that are positively associated with diseases, mortality, and aging risk factors.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge