Improving 3D Cellular Positioning Integrity with Bayesian RAIM
Paper and Code
Aug 09, 2024
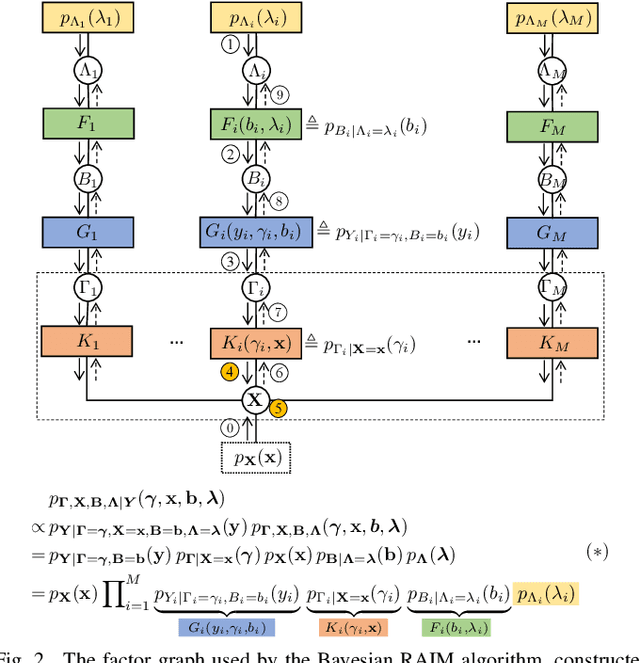
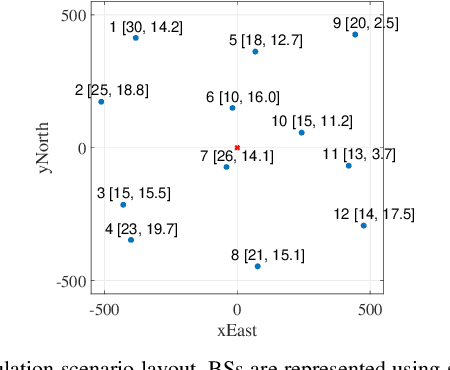
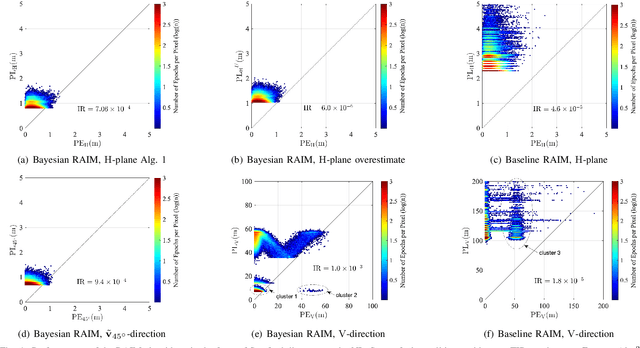
Ensuring positioning integrity amid faulty measurements is crucial for safety-critical applications, making receiver autonomous integrity monitoring (RAIM) indispensable. This paper introduces a Bayesian RAIM algorithm with a streamlined architecture for snapshot-type 3D cellular positioning. Unlike traditional frequentist-type RAIM algorithms, it computes the exact posterior probability density function (PDF) of the position vector as a Gaussian mixture (GM) model using efficient message passing along a factor graph. This Bayesian approach retains all crucial information from the measurements, eliminates the need to discard faulty measurements, and results in tighter protection levels (PLs) in 3D space and 1D/2D subspaces that meet target integrity risk (TIR) requirements. Numerical simulations demonstrate that the Bayesian RAIM algorithm significantly outperforms a baseline algorithm, achieving over $50\%$ PL reduction at a comparable computational cost.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge