Image Compression with Product Quantized Masked Image Modeling
Paper and Code
Dec 14, 2022

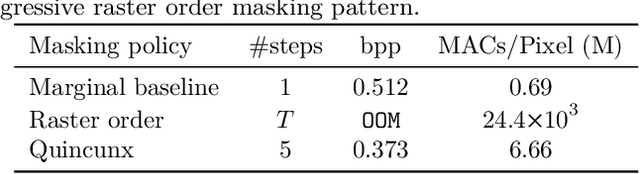

Recent neural compression methods have been based on the popular hyperprior framework. It relies on Scalar Quantization and offers a very strong compression performance. This contrasts from recent advances in image generation and representation learning, where Vector Quantization is more commonly employed. In this work, we attempt to bring these lines of research closer by revisiting vector quantization for image compression. We build upon the VQ-VAE framework and introduce several modifications. First, we replace the vanilla vector quantizer by a product quantizer. This intermediate solution between vector and scalar quantization allows for a much wider set of rate-distortion points: It implicitly defines high-quality quantizers that would otherwise require intractably large codebooks. Second, inspired by the success of Masked Image Modeling (MIM) in the context of self-supervised learning and generative image models, we propose a novel conditional entropy model which improves entropy coding by modelling the co-dependencies of the quantized latent codes. The resulting PQ-MIM model is surprisingly effective: its compression performance on par with recent hyperprior methods. It also outperforms HiFiC in terms of FID and KID metrics when optimized with perceptual losses (e.g. adversarial). Finally, since PQ-MIM is compatible with image generation frameworks, we show qualitatively that it can operate under a hybrid mode between compression and generation, with no further training or finetuning. As a result, we explore the extreme compression regime where an image is compressed into 200 bytes, i.e., less than a tweet.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge