How Powerful is Implicit Denoising in Graph Neural Networks
Paper and Code
Sep 29, 2022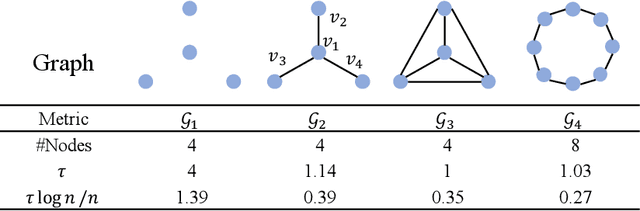
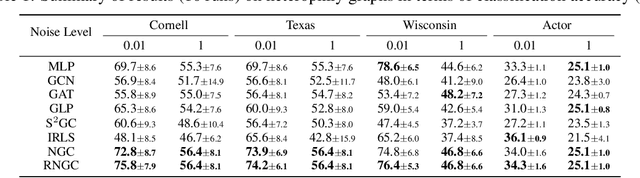
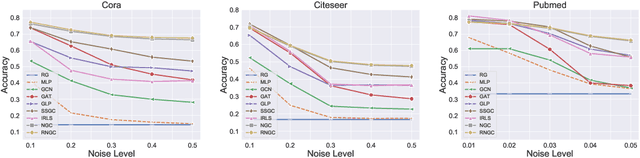
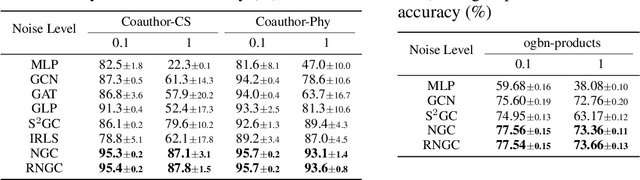
Graph Neural Networks (GNNs), which aggregate features from neighbors, are widely used for graph-structured data processing due to their powerful representation learning capabilities. It is generally believed that GNNs can implicitly remove the non-predictive noises. However, the analysis of implicit denoising effect in graph neural networks remains open. In this work, we conduct a comprehensive theoretical study and analyze when and why the implicit denoising happens in GNNs. Specifically, we study the convergence properties of noise matrix. Our theoretical analysis suggests that the implicit denoising largely depends on the connectivity, the graph size, and GNN architectures. Moreover, we formally define and propose the adversarial graph signal denoising (AGSD) problem by extending graph signal denoising problem. By solving such a problem, we derive a robust graph convolution, where the smoothness of the node representations and the implicit denoising effect can be enhanced. Extensive empirical evaluations verify our theoretical analyses and the effectiveness of our proposed model.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge