High-Order Tensor Recovery with A Tensor $U_1$ Norm
Paper and Code
Nov 23, 2023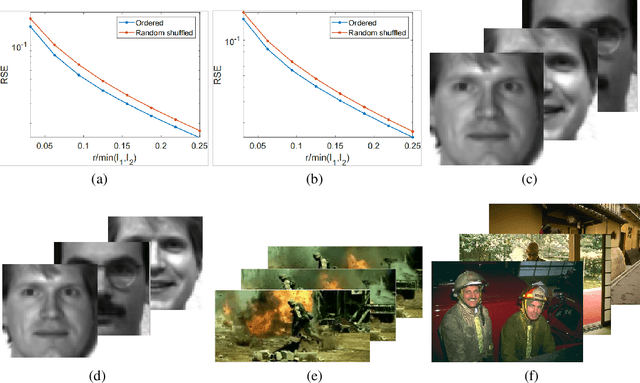


Recently, numerous tensor SVD (t-SVD)-based tensor recovery methods have emerged, showing promise in processing visual data. However, these methods often suffer from performance degradation when confronted with high-order tensor data exhibiting non-smooth changes, commonly observed in real-world scenarios but ignored by the traditional t-SVD-based methods. Our objective in this study is to provide an effective tensor recovery technique for handling non-smooth changes in tensor data and efficiently explore the correlations of high-order tensor data across its various dimensions without introducing numerous variables and weights. To this end, we introduce a new tensor decomposition and a new tensor norm called the Tensor $U_1$ norm. We utilize these novel techniques in solving the problem of high-order tensor completion problem and provide theoretical guarantees for the exact recovery of the resulting tensor completion models. An optimization algorithm is proposed to solve the resulting tensor completion model iteratively by combining the proximal algorithm with the Alternating Direction Method of Multipliers. Theoretical analysis showed the convergence of the algorithm to the Karush-Kuhn-Tucker (KKT) point of the optimization problem. Numerical experiments demonstrated the effectiveness of the proposed method in high-order tensor completion, especially for tensor data with non-smooth changes.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge