HAQJSK: Hierarchical-Aligned Quantum Jensen-Shannon Kernels for Graph Classification
Paper and Code
Nov 08, 2022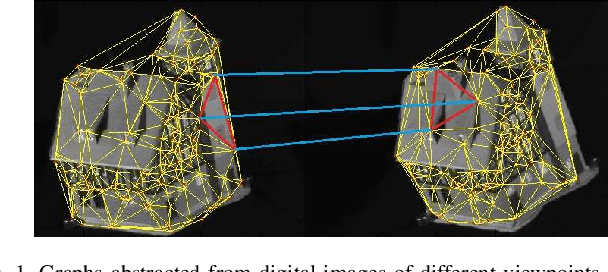
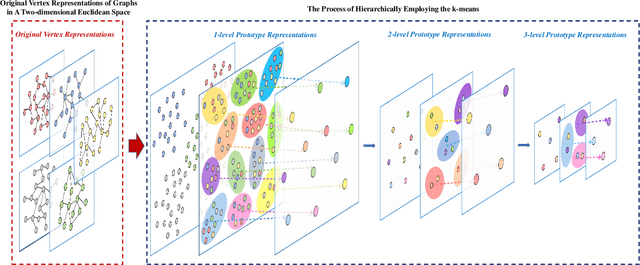
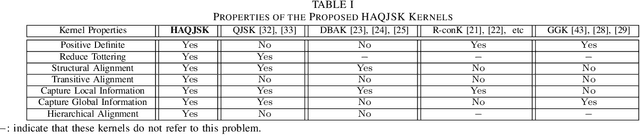
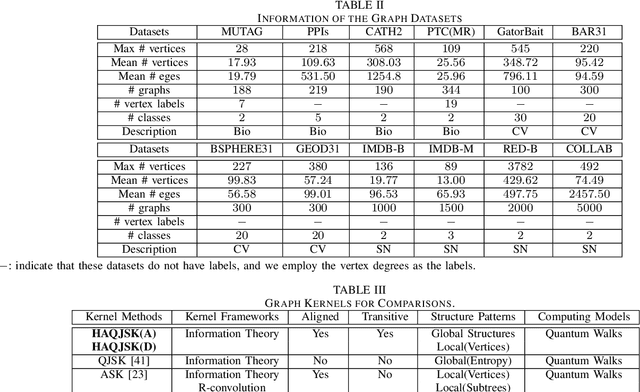
In this work, we propose a family of novel quantum kernels, namely the Hierarchical Aligned Quantum Jensen-Shannon Kernels (HAQJSK), for un-attributed graphs. Different from most existing classical graph kernels, the proposed HAQJSK kernels can incorporate hierarchical aligned structure information between graphs and transform graphs of random sizes into fixed-sized aligned graph structures, i.e., the Hierarchical Transitive Aligned Adjacency Matrix of vertices and the Hierarchical Transitive Aligned Density Matrix of the Continuous-Time Quantum Walk (CTQW). For a pair of graphs to hand, the resulting HAQJSK kernels are defined by measuring the Quantum Jensen-Shannon Divergence (QJSD) between their transitive aligned graph structures. We show that the proposed HAQJSK kernels not only reflect richer intrinsic global graph characteristics in terms of the CTQW, but also address the drawback of neglecting structural correspondence information arising in most existing R-convolution kernels. Furthermore, unlike the previous Quantum Jensen-Shannon Kernels associated with the QJSD and the CTQW, the proposed HAQJSK kernels can simultaneously guarantee the properties of permutation invariant and positive definiteness, explaining the theoretical advantages of the HAQJSK kernels. Experiments indicate the effectiveness of the proposed kernels.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge