GraphGDP: Generative Diffusion Processes for Permutation Invariant Graph Generation
Paper and Code
Dec 04, 2022

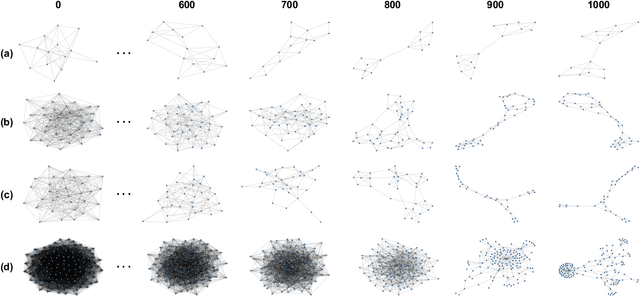

Graph generative models have broad applications in biology, chemistry and social science. However, modelling and understanding the generative process of graphs is challenging due to the discrete and high-dimensional nature of graphs, as well as permutation invariance to node orderings in underlying graph distributions. Current leading autoregressive models fail to capture the permutation invariance nature of graphs for the reliance on generation ordering and have high time complexity. Here, we propose a continuous-time generative diffusion process for permutation invariant graph generation to mitigate these issues. Specifically, we first construct a forward diffusion process defined by a stochastic differential equation (SDE), which smoothly converts graphs within the complex distribution to random graphs that follow a known edge probability. Solving the corresponding reverse-time SDE, graphs can be generated from newly sampled random graphs. To facilitate the reverse-time SDE, we newly design a position-enhanced graph score network, capturing the evolving structure and position information from perturbed graphs for permutation equivariant score estimation. Under the evaluation of comprehensive metrics, our proposed generative diffusion process achieves competitive performance in graph distribution learning. Experimental results also show that GraphGDP can generate high-quality graphs in only 24 function evaluations, much faster than previous autoregressive models.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge