Global Convolutional Neural Processes
Paper and Code
Sep 02, 2021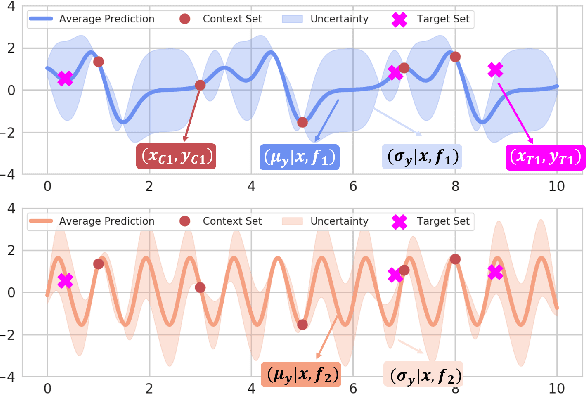
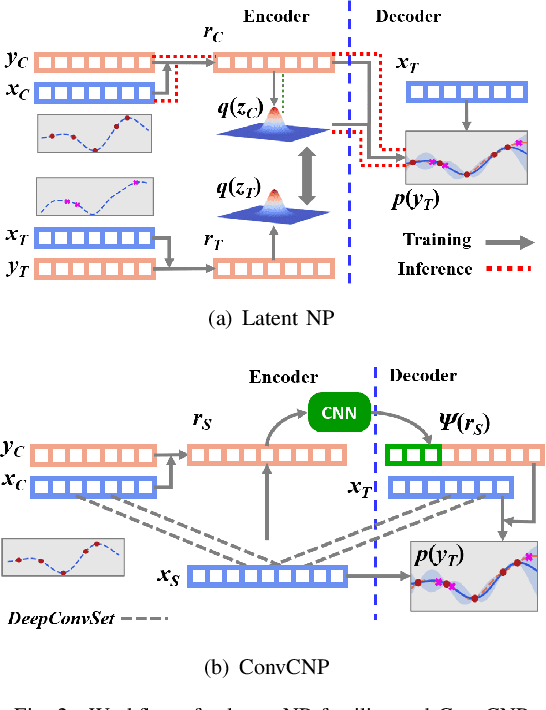
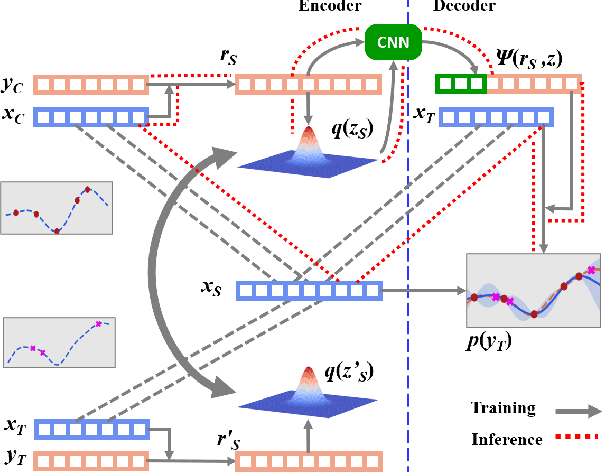
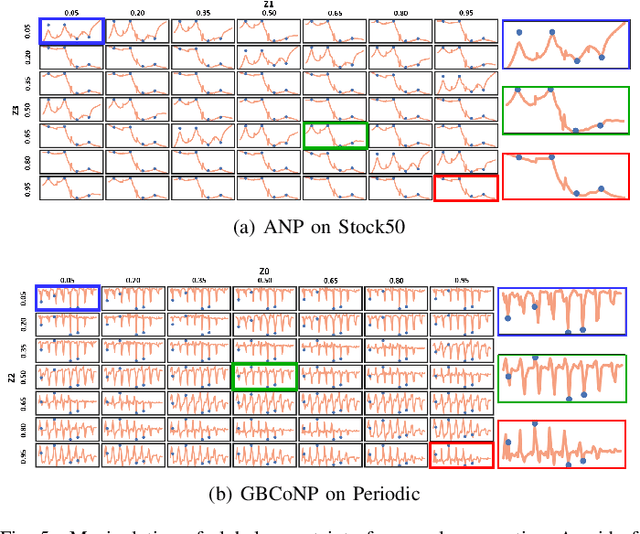
The ability to deal with uncertainty in machine learning models has become equally, if not more, crucial to their predictive ability itself. For instance, during the pandemic, governmental policies and personal decisions are constantly made around uncertainties. Targeting this, Neural Process Families (NPFs) have recently shone a light on prediction with uncertainties by bridging Gaussian processes and neural networks. Latent neural process, a member of NPF, is believed to be capable of modelling the uncertainty on certain points (local uncertainty) as well as the general function priors (global uncertainties). Nonetheless, some critical questions remain unresolved, such as a formal definition of global uncertainties, the causality behind global uncertainties, and the manipulation of global uncertainties for generative models. Regarding this, we build a member GloBal Convolutional Neural Process(GBCoNP) that achieves the SOTA log-likelihood in latent NPFs. It designs a global uncertainty representation p(z), which is an aggregation on a discretized input space. The causal effect between the degree of global uncertainty and the intra-task diversity is discussed. The learnt prior is analyzed on a variety of scenarios, including 1D, 2D, and a newly proposed spatial-temporal COVID dataset. Our manipulation of the global uncertainty not only achieves generating the desired samples to tackle few-shot learning, but also enables the probability evaluation on the functional priors.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge