Generalizing Informed Sampling for Asymptotically Optimal Sampling-based Kinodynamic Planning via Markov Chain Monte Carlo
Paper and Code
Oct 17, 2017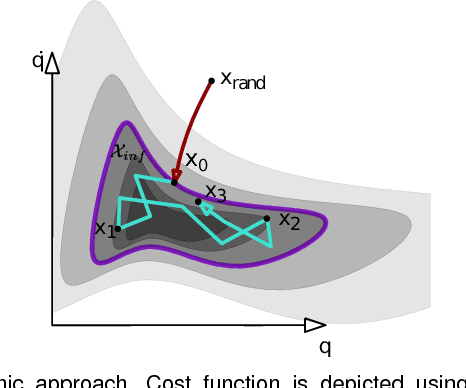
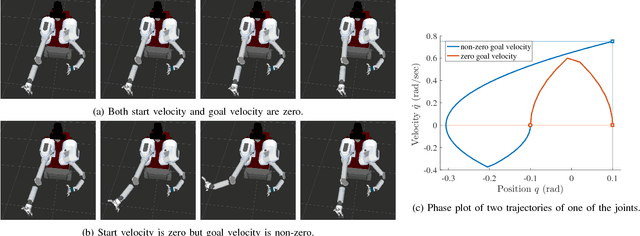
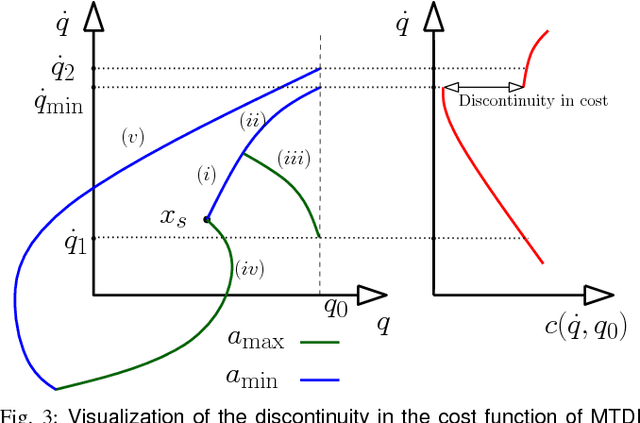
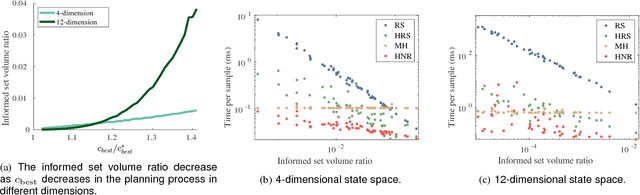
Asymptotically-optimal motion planners such as RRT* have been shown to incrementally approximate the shortest path between start and goal states. Once an initial solution is found, their performance can be dramatically improved by restricting subsequent samples to regions of the state space that can potentially improve the current solution. When the motion planning problem lies in a Euclidean space, this region $X_{inf}$, called the informed set, can be sampled directly. However, when planning with differential constraints in non-Euclidean state spaces, no analytic solutions exists to sampling $X_{inf}$ directly. State-of-the-art approaches to sampling $X_{inf}$ in such domains such as Hierarchical Rejection Sampling (HRS) may still be slow in high-dimensional state space. This may cause the planning algorithm to spend most of its time trying to produces samples in $X_{inf}$ rather than explore it. In this paper, we suggest an alternative approach to produce samples in the informed set $X_{inf}$ for a wide range of settings. Our main insight is to recast this problem as one of sampling uniformly within the sub-level-set of an implicit non-convex function. This recasting enables us to apply Monte Carlo sampling methods, used very effectively in the Machine Learning and Optimization communities, to solve our problem. We show for a wide range of scenarios that using our sampler can accelerate the convergence rate to high-quality solutions in high-dimensional problems.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge