Federated Learning with Fair Averaging
Paper and Code
May 17, 2021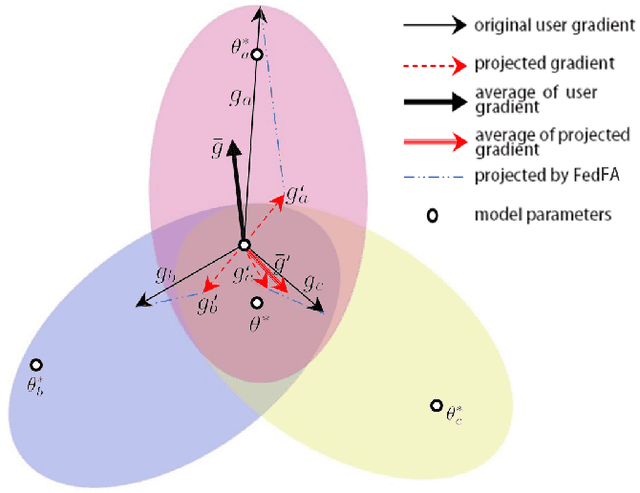
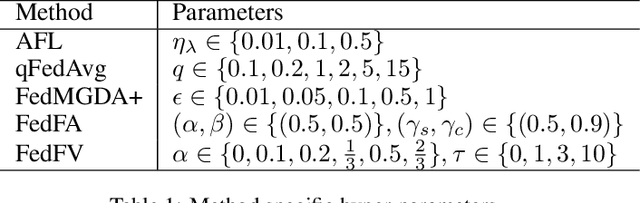
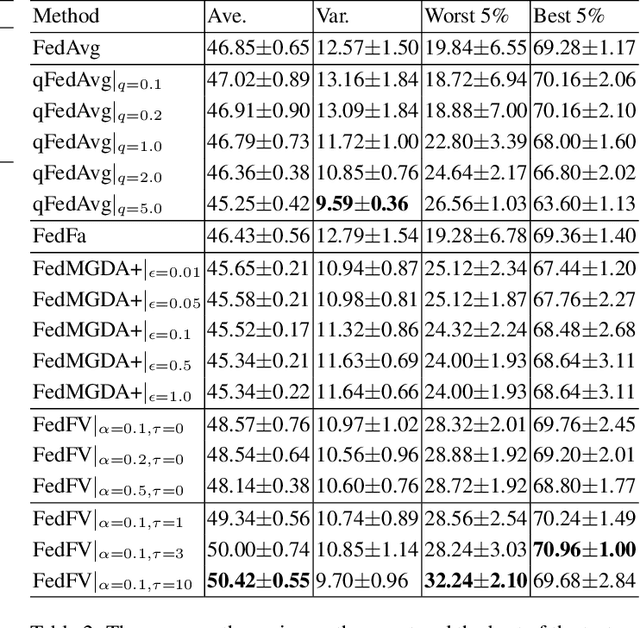
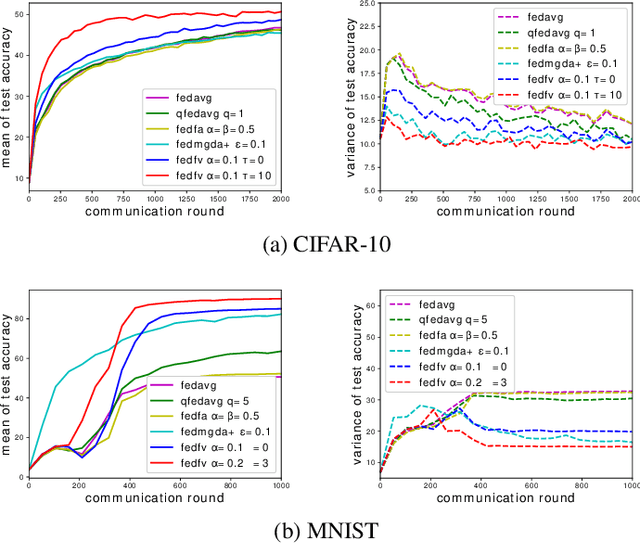
Fairness has emerged as a critical problem in federated learning (FL). In this work, we identify a cause of unfairness in FL -- \emph{conflicting} gradients with large differences in the magnitudes. To address this issue, we propose the federated fair averaging (FedFV) algorithm to mitigate potential conflicts among clients before averaging their gradients. We first use the cosine similarity to detect gradient conflicts, and then iteratively eliminate such conflicts by modifying both the direction and the magnitude of the gradients. We further show the theoretical foundation of FedFV to mitigate the issue conflicting gradients and converge to Pareto stationary solutions. Extensive experiments on a suite of federated datasets confirm that FedFV compares favorably against state-of-the-art methods in terms of fairness, accuracy and efficiency.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge