FedDRO: Federated Compositional Optimization for Distributionally Robust Learning
Paper and Code
Nov 21, 2023

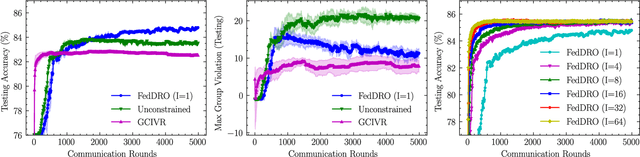
Recently, compositional optimization (CO) has gained popularity because of its applications in distributionally robust optimization (DRO) and many other machine learning problems. Large-scale and distributed availability of data demands the development of efficient federated learning (FL) algorithms for solving CO problems. Developing FL algorithms for CO is particularly challenging because of the compositional nature of the objective. Moreover, current state-of-the-art methods to solve such problems rely on large batch gradients (depending on the solution accuracy) not feasible for most practical settings. To address these challenges, in this work, we propose efficient FedAvg-type algorithms for solving non-convex CO in the FL setting. We first establish that vanilla FedAvg is not suitable to solve distributed CO problems because of the data heterogeneity in the compositional objective at each client which leads to the amplification of bias in the local compositional gradient estimates. To this end, we propose a novel FL framework FedDRO that utilizes the DRO problem structure to design a communication strategy that allows FedAvg to control the bias in the estimation of the compositional gradient. A key novelty of our work is to develop solution accuracy-independent algorithms that do not require large batch gradients (and function evaluations) for solving federated CO problems. We establish $\mathcal{O}(\epsilon^{-2})$ sample and $\mathcal{O}(\epsilon^{-3/2})$ communication complexity in the FL setting while achieving linear speedup with the number of clients. We corroborate our theoretical findings with empirical studies on large-scale DRO problems.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge